��Ŀ����
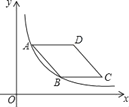
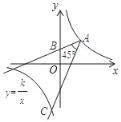
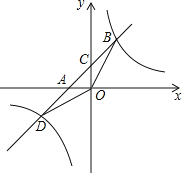
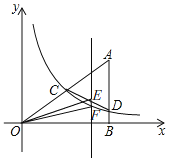
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��ABO�ı�AB��ֱ��x�ᣬ����Ϊ��B������������y��![]() (x��0)��ͼ��AO���е�C����AB�ڵ�D����AD��3��
(x��0)��ͼ��AO���е�C����AB�ڵ�D����AD��3��
(1)���A������Ϊ(4��4)���C������Ϊ�� ����
(2)����D������Ϊ(4��n)��
����������y��![]() �ı���ʽ��
�ı���ʽ��
����C��D�����ֱ������Ӧ�ĺ�������ʽ��
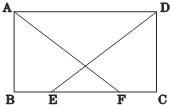
(3)��(2)�������£����E���߶�CD�ϵĶ���(�����C��D�غ�)������E��ƽ��y���ֱ��l�뷴����������ͼ���ڵ�F�����OEF��������ֵ��

���𰸡�(1)C(2��2)��(2)�ٷ�������������ʽΪy��![]() ����ֱ��CD�Ľ���ʽΪy����
����ֱ��CD�Ľ���ʽΪy����![]() x+3��(3)m��3ʱ��S��OEF������ֵΪ
x+3��(3)m��3ʱ��S��OEF������ֵΪ![]() .
.
��������
��1�������е����깫ʽ���ɵó����ۣ�
��2������ȷ������A���꣬�����ó���C���꣬����C��D������뷴���������м��ɵó����ۣ�
����n=1�������C��D���꣬���ô���ϵ�������ɵó����ۣ�
��3�������E���꣬������ʾ����F���꣬���ɽ��������m�ĺ�����ϵʽ���ɵó����ۣ�
(1)�ߵ�C��OA���е㣬A(4��4)��O(0��0)��
��C![]() ��
��
��C(2��2)��
�ʴ�Ϊ(2��2)��
(2)����AD��3��D(4��n)��
��A(4��n+3)��
�ߵ�C��OA���е㣬
��C(2��![]() )��
)��
�ߵ�C��D(4��n)��˫����![]() �ϣ�
�ϣ�
��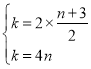 ��
��
��![]() ��
��
�෴������������ʽΪ![]() ��
��
������֪��n��1��
��C(2��2)��D(4��1)��
��ֱ��CD�Ľ���ʽΪy��ax+b��
��![]() ��
��
��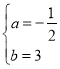 ��
��
��ֱ��CD�Ľ���ʽΪy����![]() x+3��
x+3��
(3)��ͼ����(2)֪��ֱ��CD�Ľ���ʽΪy����![]() x+3��
x+3��
���E(m����![]() m+3)��
m+3)��
��(2)֪��C(2��2)��D(4��1)��
��2��m��4��
��EF��y�ύ˫����![]() ��F��
��F��
��F(m��![]() )��
)��
��EF����![]() m+3��
m+3��![]() ��
��
��S��OEF��![]() (��
(��![]() m+3��
m+3��![]() )��m��
)��m��![]() (��
(��![]() m2+3m��4)����
m2+3m��4)����![]() (m��3)2+
(m��3)2+![]() ��
��
��2��m��4��
��m��3ʱ��S��OEF������ֵΪ![]()


 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�