��Ŀ����
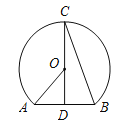
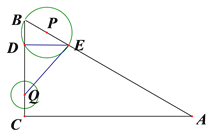
����Ŀ����ͼ���ڡ�ABC�У���ACBΪֱ�ǣ�AB=10��![]() �㣬�뾶Ϊ1�Ķ�ԲQ��Բ�Ĵӵ�C����������CB������1����λ����/����ٶ������˶���ͬʱ����P�ӵ�B����������BA����Ҳ��1����λ����/����ٶ������˶������˶�ʱ��Ϊt�루0��t��5����PΪԲ�ģ�PB��Ϊ�뾶�ġ�P��AB��BC����һ������ֱ�ΪE��D������ED��EQ��
�㣬�뾶Ϊ1�Ķ�ԲQ��Բ�Ĵӵ�C����������CB������1����λ����/����ٶ������˶���ͬʱ����P�ӵ�B����������BA����Ҳ��1����λ����/����ٶ������˶������˶�ʱ��Ϊt�루0��t��5����PΪԲ�ģ�PB��Ϊ�뾶�ġ�P��AB��BC����һ������ֱ�ΪE��D������ED��EQ��
��1���жϲ�֤��ED��BC��λ�ù�ϵ������Q���D�غ�ʱt��ֵ��
��2������P��AC�ཻʱ����CQΪ![]() ����P��AC �صõ��ҳ�Ϊ
����P��AC �صõ��ҳ�Ϊ![]() ����
����![]() ����
����![]() �ĺ����� ����Q����Bʱ��P��AC�صõ��ҳ���
�ĺ����� ����Q����Bʱ��P��AC�صõ��ҳ���
��3������P���Q�ཻ��д��t��ȡֵ��Χ��

���𰸡���1��ED��BC��![]() ����2��
����2��![]() ��
��![]() ����3��
����3��![]()
�������������������1������PD����PB=PD��PD=PE���ɵá�PBD=��PDB����PDE=��PED�����������ε��ڽǺͶ����ɵ���BDE=��BDP+��PDE=90�㣬���ɵ�DE��BC����DE��CA���ɵá�BDE�ס�BCA���������������ε����ʿɵ�![]() ����CQ=CD=t��BD=5-t��BE=2t���������tֵ���ɣ����P��AC�ཻ�� M��N��BP=CQ=x��AP=AB-BP=10-x,����P��PH��AC�ڵ� H,��Rt��APH�У��ɵ�PH=
����CQ=CD=t��BD=5-t��BE=2t���������tֵ���ɣ����P��AC�ཻ�� M��N��BP=CQ=x��AP=AB-BP=10-x,����P��PH��AC�ڵ� H,��Rt��APH�У��ɵ�PH=![]() AP��PH=
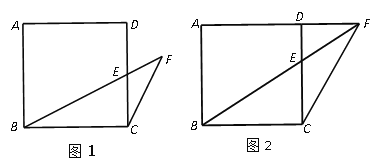
AP��PH=![]() (10-x)����Rt��PHN�У��������y����x�ĺ�������ͼ������Q����B��ʱ�� CQ=CB��QB=4����t��ֵ���뼴�����MN�ij�����3����Q��P���Q����ʱ����ͼ����ʱ��֪��QBP=60�㣬BQ=5-t��PQ=t+1��BP=t��
(10-x)����Rt��PHN�У��������y����x�ĺ�������ͼ������Q����B��ʱ�� CQ=CB��QB=4����t��ֵ���뼴�����MN�ij�����3����Q��P���Q����ʱ����ͼ����ʱ��֪��QBP=60�㣬BQ=5-t��PQ=t+1��BP=t��![]() ����Ӵ�ʱ��ֱ��ֹͣ�˶�����P���Q�������ཻλ�ã����ɵá�P���Q�ཻʱt��ȡֵ��Χ.
����Ӵ�ʱ��ֱ��ֹͣ�˶�����P���Q�������ཻλ�ã����ɵá�P���Q�ཻʱt��ȡֵ��Χ.
���������
��1������PD����B��E��D���ڡ�P��
��PB=PD����PBD=��PDB�� PD=PE����PDE=��PED
�ߡ�BDE���ڽǺ�Ϊ180�� ���BDE=��BDP+��PDE=90�㣬
�༴��DE��BC
�ߡ�BCA=90�㣬![]() ��
��
��DE��CA�����BDE�ס�BCA��
��![]()
��CQ=CD=t��BD=5-t��BE=2t
������![]() ��ã�
��ã�![]()
�൱![]() ʱQ��D�غ�.
ʱQ��D�غ�.
��2�����P��AC�ཻ�� M��N��

BP=CQ=x��AP=AB-BP=10-x����P��PH��
��Rt��APH�У���֪��![]()
PH=![]()
��Rt��PHN�У���֪��HN=![]() =
=![]()
![]()
����Q����B��ʱ������ͼ�� CQ=CB��QB=4��

��![]() ����ã�
����ã�![]()
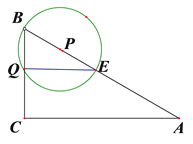
��3����Q��P���Q����ʱ����ͼ��
��֪��ʱ��QBP=60�㣬BQ=5-t��PQ=t+1��BP=t
![]() ��
��
�ߴӴ�ʱ��ֱ��ֹͣ�˶�����P���Q�������ཻλ��
���P���Q�ཻʱt��ȡֵ��ΧΪ�� ![]()

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�