题目内容
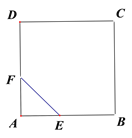
【题目】如图,E、F分别为正方形ABCD的边AB、AD上的点,且AE=AF,联接EF,将△AEF绕点A逆时针旋转45°,使E落在E![]() ,F落在F
,F落在F![]() ,联接BE
,联接BE![]() 并延长交DF
并延长交DF![]() 于点G,如果AB=
于点G,如果AB=![]() ,AE=1,则DG=______.
,AE=1,则DG=______.
【答案】![]()
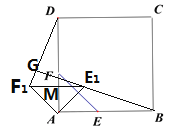
【解析】在Rt△AEF中,由勾股定理可得EF=![]() ,把△AEF绕点A逆时针旋转45°可得△AE1F1,可得E1F1=EF=
,把△AEF绕点A逆时针旋转45°可得△AE1F1,可得E1F1=EF=![]() ,∠E1AM=45°,可得AM=F1M=
,∠E1AM=45°,可得AM=F1M=![]() ,因AB=
,因AB=![]() ,可得DM=
,可得DM=![]() ,在Rt△DMF1中,由勾股定理可得DF1=
,在Rt△DMF1中,由勾股定理可得DF1=![]() ,利用SAS证明△ABE1≌△ADF1,根据全等三角形的性质可得∠E1BA=∠ADF1,由此易证BG⊥DF1,因E1F1∥AB,根据平行线的性质可得∠E1BA=∠GE1F1,所以∠ADF1=∠GE1F1,即可证明△GE1F1∽△MDF1,根据相似三角形的性质可得
,利用SAS证明△ABE1≌△ADF1,根据全等三角形的性质可得∠E1BA=∠ADF1,由此易证BG⊥DF1,因E1F1∥AB,根据平行线的性质可得∠E1BA=∠GE1F1,所以∠ADF1=∠GE1F1,即可证明△GE1F1∽△MDF1,根据相似三角形的性质可得![]() ,即
,即![]() ,解得F1G=
,解得F1G=![]() ,所以DG=DF1-F1G=
,所以DG=DF1-F1G=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目