Question

【题目】已知：正方形，点在边上，点在线段的延长线上，且.

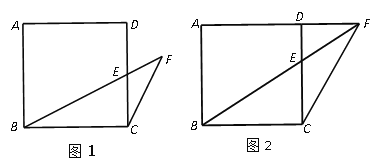
（1）如图1，当点为边的中点时，求证：；

（2）如图2，当点位于线段的延长线上，求证：.

Answer 1

【答案】(1)证明见解析；（2）证明见解析.

【解析】（1）由正方形性质和相似三角形证明等量关系式；（2）正方形的性质得出平行关系，得到角相等，由△FDE∽△CDF得到比例式.

（1）证明：∵四边形是正方形，∴.

∵点为边的中点，∴ .

∵，，∴△FCE∽△FBC.

∴.

又∵，∴.即.

（2）∵四边形是正方形，∴∥，∥，=.

∵点位于线段的延长线上，∥，∴.

又∵=，∴.

∵∥，∴.

又∵，∴.

又∵，∴△FDE∽△CDF.

∴

∴

“点睛”本题主要考查了正方形的性质，相似三角形性质，解题关键是由已知条件作出两对角相等.