题目内容
【题目】已知实数a,b满足(2a+1)2+|a+b+1|=0,且关于x,y的方程组![]() 的解x<0,y>0,求m的取值范围.
的解x<0,y>0,求m的取值范围.
【答案】解:∵(2a+1)2+|a+b+1|=0,
∴2a+1=0,a+b+1=0,
解得:a=![]() , b=
, b=![]() ,
,
代入方程组![]() 得:
得: ,
,
解得:x=![]() , y=
, y=![]() ,
,
, ∵x<0,y>0,
∴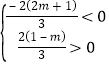 ,
,
解不等式组得:![]() <m<1,
<m<1,
即m的取值范围是:![]() <m<1.
<m<1.
【解析】根据偶次方,绝对值得出2a+1=0,a+b+1=0,求出a、b的值,代入方程组得出关于x、y的方程组,求出法则的解,根据x<0,y>0得出关于m的不等式组,求出不等式组的解集即可.
【考点精析】根据题目的已知条件,利用二元一次方程的解和一元一次不等式组的解法的相关知识可以得到问题的答案,需要掌握适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).

练习册系列答案
相关题目