题目内容
【题目】如图所示,点D是弦AB的中点,点C在⊙O上,CD经过圆心O,则下列结论中不一定正确的是( )
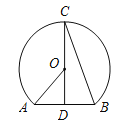
A. CD⊥AB B. ∠OAD =2∠CBD C. ∠AOD =2∠BCD D. 弧AC = 弧BC
【答案】B
【解析】根据垂线定理及圆周角定理进行解答即可.
解:∵点D是弦AB的中点,CD经过圆心O,∴∠CD⊥AB,弧AC = 弧BC,故A、D正确;
∵弧AC = 弧BC,等弧所对的圆心角∠AOD是∠BCD所对圆周角的2倍,∴∠OAD =2∠CBD不正确;
∵等弧所对的圆心角∠AOD是∠BCD所对圆周角的2倍,∴∠AOD =2∠BCD正确,
故选B.
“点睛”本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧,等弧所对的圆心角是所对圆周角的2倍是解答此题的关键.

练习册系列答案
相关题目