题目内容
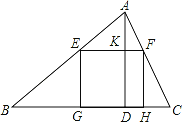
【题目】如图,一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,设EG=x mm,EF=y mm.
(1)写出x与y的关系式;
(2)用S表示矩形EGHF的面积,某同学说当矩形EGHF为正方形时S最大,这个说法正确吗?说明理由,并求出S的最大值.
【答案】(1)y=120-![]() x;(2)当矩形EGHF为正方形时S最大,这个说法是错误的. x=40mm,y=60mm时,矩形EGHF的面积最大,最大面积为2400平方毫米.
x;(2)当矩形EGHF为正方形时S最大,这个说法是错误的. x=40mm,y=60mm时,矩形EGHF的面积最大,最大面积为2400平方毫米.
【解析】
(1)易证△AEF∽△ABC,根据相似三角形对应边的比等于对应高的比,即可求解;
(2)矩形EGHF的面积S=xy,根据(1)中y与x的函数关系式,即可得到S与x之间的函数关系,根据函数的性质即可求解;
根据已知条件易知:EF∥BC,AD⊥EF,PN=GH=ymm,DK=EG=xmm,
∴△AEF∽△ABC.
从而有![]() ,即
,即![]() ,
,
∴y=120-![]() x;
x;
(2)设矩形EGHF的面积为S,则S=xy,
即S=x(120-![]() x),
x),
当x=-![]() =40时,S有最大值为2400
=40时,S有最大值为2400
此时y=![]() =60
=60
∴x=40mm,y=60mm时,矩形EGHF的面积最大,最大面积为2400平方毫米.
故当矩形当矩形EGHF为正方形时S最大,这个说法是错误的.为正方形时S最大,这个说法是错误的.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目