题目内容
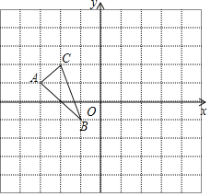
【题目】如图所示,已知抛物线![]() 的图像经过点A(1,0),B(0,5),
的图像经过点A(1,0),B(0,5),

(1)求这个抛物线的解析式;
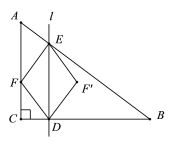
(2)设(1)中的抛物线与x轴的另一个交点为C,求出点C的坐标;并确定在抛物线上是否存在一点E,使△BCE是以BC为斜边的直角三角形?若存在,在图中做出所有的点E(不写画法,保留作图痕迹);若不存在,说明理由;
(3)点P是直线BC上的一个动点(P点不与B点和C点重合),过点P做x轴的垂线,交抛物线于点M,点Q在直线BC上,距离点P为![]() 个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式。
个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式。
【答案】(1)![]() ;(2)点C的坐标是(-5,0),存在,图形详见解析;(3)
;(2)点C的坐标是(-5,0),存在,图形详见解析;(3)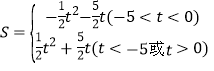 .
.
【解析】
(1)将点A、点B的坐标代入抛物线解析式可得出b、c的值,继而得出抛物线解析式;
(2)根据抛物线解析式求出点C的坐标,以BC的中点D为圆心,以![]() BC为半径画圆,与抛物线有两个交点E和E′;
BC为半径画圆,与抛物线有两个交点E和E′;
(3)由点B的坐标为(0,5),点C的坐标为(-5,0),可得直线BC的解析式为y=x+5.
设P的坐标为(t,t+5),则点M的坐标(t,![]() ).过点Q作QF⊥PM于点F,则△PQF为等腰直角三角形,得到QF=1.然后分两种情况讨论:①当点P在点M下方时,即-5﹤t﹤0时,②当点P在点M上方时,t﹤-5或t>0时,分别表示出PM,然后求出△PMQ的面积即可.
).过点Q作QF⊥PM于点F,则△PQF为等腰直角三角形,得到QF=1.然后分两种情况讨论:①当点P在点M下方时,即-5﹤t﹤0时,②当点P在点M上方时,t﹤-5或t>0时,分别表示出PM,然后求出△PMQ的面积即可.
(1)将点A(1,0)、点B(0,5)代入抛物线y=﹣x2+bx+c可得:![]() ,解得:
,解得:![]() ,故抛物线解析式为:y=﹣x2﹣4x+5.
,故抛物线解析式为:y=﹣x2﹣4x+5.
(2)由y=﹣x2﹣4x+5,令y=0,得:﹣x2﹣4x+5=0,解得:x1=﹣5,x2=1,则点C的坐标为(﹣5,0),若在抛物线上存在点E,使△BCE是以BC为斜边的直角三角形,则∠BEC=90°,即点E是以BC为直径的圆与抛物线的交点.如图:
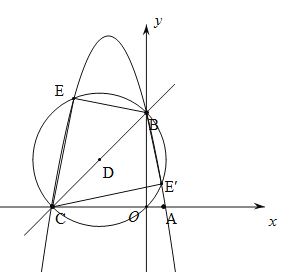
(3)由点B的坐标为(0,5),点C的坐标为(-5,0),∴可得直线BC的解析式为y=x+5.
∵点P的横坐标为t,PM⊥x轴,∴点M的横坐标为t.
又点P在直线BC上,点M在抛物线上,∴所以点P的坐标为(t,t+5),点M的坐标(t,![]() ).
).
过点Q作QF⊥PM于点F,则△PQF为等腰直角三角形.
∵![]() ∴QF=1.
∴QF=1.
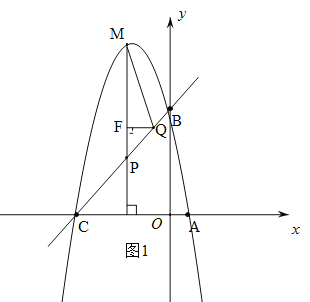
当点P在点M下方时,即-5﹤t﹤0时,如图1,![]() ,∴
,∴![]() ;
;
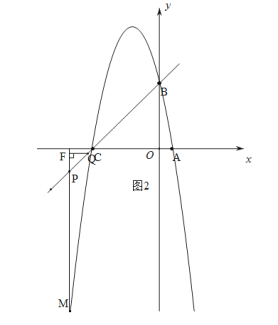
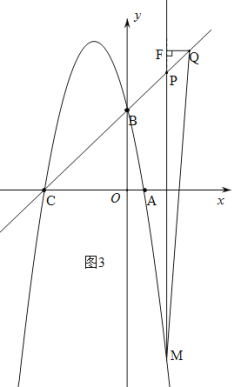
当点P在点M上方时,t﹤-5或t>0时,如图2,图3,![]() ,∴
,∴![]() .
.
综上所述: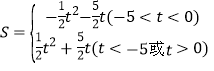 .
.

 53随堂测系列答案
53随堂测系列答案