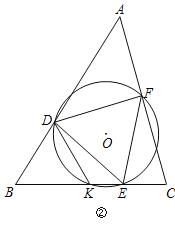ЬтФПФкШн
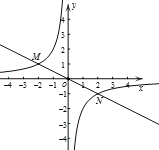
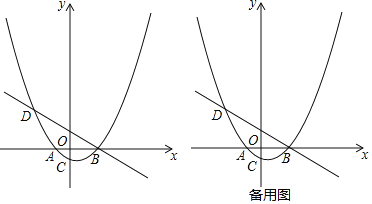
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=aЃЈx+2ЃЉЃЈx-4ЃЉЃЈaЮЊГЃЪ§ЃЌЧвaЃО0ЃЉгыxжсДгзѓжСгввРДЮНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкЕуCЃЌОЙ§ЕуBЕФжБЯпy=-![]() x+bгыХзЮяЯпЕФСэвЛНЛЕуЮЊDЃЌЧвЕуDЕФКсзјБъЮЊ-5ЃЎ
x+bгыХзЮяЯпЕФСэвЛНЛЕуЮЊDЃЌЧвЕуDЕФКсзјБъЮЊ-5ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉPЮЊжБЯпBDЯТЗНЕФХзЮяЯпЩЯЕФвЛЕуЃЌСЌНгPDЁЂPBЃЌЧѓЁїPBDУцЛ§ЕФзюДѓжЕЃЛ
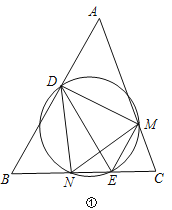
ЃЈ3ЃЉЩшFЮЊЯпЖЮBDЩЯвЛЕуЃЈВЛКЌЖЫЕуЃЉЃЌСЌНгAFЃЌвЛЖЏЕуMДгЕуAГіЗЂЃЌбиЯпЖЮAFвдУПУы1ИіЕЅЮЛЕФЫйЖШдЫЖЏЕНFЃЌдйбиЯпЖЮFDвдУПУы2ИіЕЅЮЛЕФЫйЖШдЫЖЏЕНDКѓЭЃжЙЃЌЕБЕуFЕФзјБъЪЧЖрЩйЪБЃЌЕуMдкећИідЫЖЏЙ§ГЬжагУЪБзюЩйЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЃЈ-2ЃЌ2
ЃЛЃЈ3ЃЉЃЈ-2ЃЌ2![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШЧѓГіЕуAЁЂBзјБъЃЌШЛКѓЧѓГіжБЯпBDЕФНтЮіЪНЃЌЧѓЕУЕуDзјБъЃЌДњШыХзЮяЯпНтЮіЪНЃЌЧѓЕУaЕФжЕЃЛ
ЃЈ2ЃЉгУШ§НЧаЮЕФУцЛ§ЙЋЪННЈСЂКЏЪ§ЙиЯЕЪНЃЌдйШЗЖЈГізюДѓжЕЃЛ
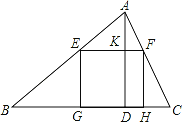
ЃЈ3ЃЉгЩЬтвтЃЌЖЏЕуMдЫЖЏЕФТЗОЖЮЊелЯпAF+DFЃЌдЫЖЏЪБМфЃКt=AF+![]() DFЃЎШчЭМЃЌзїИЈжњЯпЃЌНЋAF+
DFЃЎШчЭМЃЌзїИЈжњЯпЃЌНЋAF+![]() DFзЊЛЏЮЊAF+FGЃЛдйгЩДЙЯпЖЮзюЖЬЃЌЕУЕНДЙЯпЖЮAHгыжБЯпBDЕФНЛЕуЃЌМДЮЊЫљЧѓЕФFЕуЃЎ
DFзЊЛЏЮЊAF+FGЃЛдйгЩДЙЯпЖЮзюЖЬЃЌЕУЕНДЙЯпЖЮAHгыжБЯпBDЕФНЛЕуЃЌМДЮЊЫљЧѓЕФFЕуЃЎ
ЃЈ1ЃЉХзЮяЯпy=aЃЈx+2ЃЉЃЈx-4ЃЉЃЌСюy=0ЃЌНтЕУx=-2Лђx=4ЃЌ
ЁрAЃЈ-2ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЎ
ЁпжБЯпy=-![]() x+bОЙ§ЕуBЃЈ4ЃЌ0ЃЉЃЌ
x+bОЙ§ЕуBЃЈ4ЃЌ0ЃЉЃЌ
Ёр-![]() ЁС4+b=0ЃЌНтЕУb=
ЁС4+b=0ЃЌНтЕУb=![]() ЃЌ
ЃЌ
ЁржБЯпBDНтЮіЪНЮЊЃКy=-![]() x+
x+![]() ЃЌ
ЃЌ
ЕБx=-5ЪБЃЌy=3![]() ЃЌ
ЃЌ
ЁрDЃЈ-5ЃЌ3![]() ЃЉЃЌ
ЃЉЃЌ
ЁпЕуDЃЈ-5ЃЌ3![]() ЃЉдкХзЮяЯпy=aЃЈx+2ЃЉЃЈx-4ЃЉЩЯЃЌ
ЃЉдкХзЮяЯпy=aЃЈx+2ЃЉЃЈx-4ЃЉЩЯЃЌ
ЁрaЃЈ-5+2ЃЉЃЈ-5-4ЃЉ=3![]() ЃЌ
ЃЌ
Ёрa=![]() ЃЎ
ЃЎ
ЁрХзЮяЯпЕФКЏЪ§БэДяЪНЮЊЃКy=![]() x2-
x2-![]() x-
x-![]()
ЃЈ2ЃЉЩшPЃЈmЃЌ![]() m2-
m2-![]() m-
m-![]() ЃЉ
ЃЉ
ЁрSЁїBPD=![]() ЁС9[ЃЈ-
ЁС9[ЃЈ-![]() m+
m+![]() ЃЉ-ЃЈ
ЃЉ-ЃЈ![]() m2-
m2-![]() m-
m-![]() ЃЉ]
ЃЉ]
=-![]() m2-
m2-![]() m+10
m+10![]()
=-![]() ЃЈm+
ЃЈm+![]() ЃЉ2+
ЃЉ2+![]()
ЁрЁїBPDУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
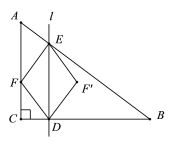
ЃЈ3ЃЉШчЭМЃЌ

зїDKЁЮABЃЌAHЁЭDKЃЌAHНЛжБЯпBDгкЕуFЃЌ
ЁпгЩЃЈ2ЃЉЕУЃЌDN=3![]() ЃЌBN=9ЃЌ
ЃЌBN=9ЃЌ
ЁпЁЯDBA=30ЁуЃЌ
ЁрЁЯBDH=30ЁуЃЌ
ЁрFG=DFЁСsin30Ёу=![]() FDЃЌ
FDЃЌ
ЁрЕБЧвНіЕБAHЁЭDKЪБЃЌAF+FHзюаЁЃЌ
ЕуMдкећИідЫЖЏжагУЪБЮЊЃКt=AF+![]() FD=AF+FHЃЌ
FD=AF+FHЃЌ
ЁпlBDЃКy=-![]() x+
x+![]() ЃЌ
ЃЌ
ЁрFx=Ax=-2ЃЌFЃЈ-2ЃЌ2![]() ЃЉ
ЃЉ
ЁрЕБFзјБъЮЊЃЈ-2ЃЌ2![]() ЃЉЪБЃЌгУЪБзюЩйЃЎ
ЃЉЪБЃЌгУЪБзюЩйЃЎ

ЁОЬтФПЁПФГЙЋЫОЩњВњЕФФГжжВњЦЗУПМўГЩБОЮЊ40дЊЃЌОЪаГЁЕїВщећРэГіШчЯТаХЯЂЃК
ЂйИУВњЦЗ90ЬьФкШеЯњЪлСПЃЈmМўЃЉгыЪБМфЃЈЕкxЬьЃЉТњзувЛДЮКЏЪ§ЙиЯЕЃЌВПЗжЪ§ОнШчЯТБэЃК
ЪБМфЃЈЕкxЬьЃЉ | 1 | 3 | 6 | 10 | Ё |
ШеЯњЪлСПЃЈmМўЃЉ | 198 | 194 | 188 | 180 | Ё |
ЂкИУВњЦЗ90ЬьФкУПЬьЕФЯњЪлМлИёгыЪБМфЃЈЕкxЬьЃЉЕФЙиЯЕШчЯТБэЃК
ЪБМфЃЈЕкxЬьЃЉ | 1ЁмxЃМ50 | 50ЁмxЁм90 |
ЯњЪлМлИёЃЈдЊ/МўЃЉ | x+60 | 100 |
ЃЈ1ЃЉЧѓmЙигкxЕФвЛДЮКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЩшЯњЪлИУВњЦЗУПЬьРћШѓЮЊyдЊЃЌЧыаДГіyЙигкxЕФКЏЪ§БэДяЪНЃЌВЂЧѓГідк90ЬьФкИУВњЦЗФФЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃПЁОЬсЪОЃКУПЬьЯњЪлРћШѓ=ШеЯњЪлСПЁСЃЈУПМўЯњЪлМлИё-УПМўГЩБОЃЉЁП
ЃЈ3ЃЉдкИУВњЦЗЯњЪлЕФЙ§ГЬжаЃЌЙВгаЖрЩйЬьЯњЪлРћШѓВЛЕЭгк5400дЊЃЌЧыжБНгаДГіНсЙћЃЎ