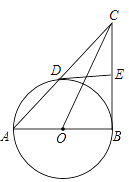
[题目]如图.在△ABC中.AC=3.BC=4.若AC.BC边上的中线BE,AD垂直相交于点O.则AB= . 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在△ABC中，AC=3，BC=4，若AC，BC边上的中线BE,AD垂直相交于点O，则AB=______.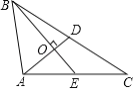

【答案】

【解析】

利用三角形中线定义得到BD=2，AE=，且可判定点O为△ABC的重心，所以AO=2OD，OB=2OE，利用勾股定理得到BO2+OD2=4，OE2+AO2=，等量代换得到BO2+ AO2=4，BO2+AO2=，把两式相加得到BO2+AO2=5，然后再利用勾股定理可计算出AB的长．

解：∵AD、BE为AC，BC边上的中线，
∴BD=BC=2，AE=AC=，点O为△ABC的重心，
∴AO=2OD，OB=2OE，
∵BE⊥AD，
∴BO2+OD2=BD2=4，OE2+AO2=AE2=，
∴BO2+AO2=4，BO2+AO2=，
∴BO2+AO2= ，
∴BO2+AO2=5，
∴AB==．
故答案是：．

练习册系列答案

将相邻三个面的面积记为S1、S2、S3，且S1＜S2＜S3的小长方体称为单位长方体，现将若干个单位长方体在空间直角坐标系内进行码放，要求码放时将单位长方体S1所在的面与x轴垂直，S2所在的面与y轴垂直，S3所在的面与z轴垂直，如图1所示.

若将x轴方向表示的量称为几何体码放的排数，y轴方向表示的量称为几何体码放的列数，z轴方向表示的量称为几何体码放的层数；如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体，其中这个几何体共码放了1排2列6层，用有序数组记作（1,2,6），如图3的几何体码放了2排3列4层，用有序数组记作（2,3,4）.这样我们就可用每一个有序数组（x，y，z）表示一种几何体的码放方式.

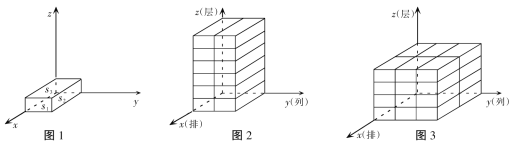
（1）如图是由若干个单位长方体码放的一个几何体的三视图，写出这种码放方式的有序数组，组成这个几何体的单位长方体的个数为多少个；

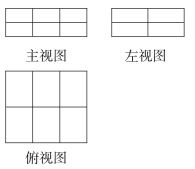
（2）对有序数组性质的理解，下列说法正确的是哪些；（只写序号）

①每一个有序数组（x，y，z）表示一种几何体的码放方式.

②有序数组中x、y、z的乘积就表示几何体中单位长方体的个数.

③有序数组不同，所表示几何体的单位长方体个数不同.

④不同的有序数组所表示的几何体的体积不同.

⑤有序数组中x、y、z每两个乘积的2倍可分别确定几何体表面上S1、S2、S3的个数.

（3）为了进一步探究有序数组（x，y，z）的几何体的表面积公式S（x,y,z），某同学针对若干个单位长方体进行码放，制作了下列表格：

几何体有序数组	单位长方体的个数	表面上面积为的个数	表面上面积为的个数	表面上面积为的个数	表面积
(1，1，1)	1	2	2	2	2S1+2S2+2S3
(1，2，1)	2	4	2	4	4S1+2S2+4S3
(3，1，1)	3	2	6	6	2S1+6S2+6S3
(2，1，2)	4	4	8	4	4S1+8S2+4S3
(1，5，1)	5	10	2	10	10S1+2S2+10S3
(1，2，3)	6	12	6	4	12S1+6S2+4S3
(1，1，7)	7	14	14	2	14S1+14S2+2S3
(2，2，2)	8	8	8	8	8S1+8S2+8S3
…	…	…	…	…	…