题目内容
【题目】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
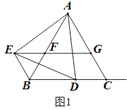
(1) 如图1,当点D在线段BC上时:
①求证:△AEB≌△ADC;②求证:四边形BCGE是平行四边形;
(2)如图2,当点D在BC的延长线上,且CD=BC时,试判断四边形BCGE是什么特殊的四边形?并说明理由.
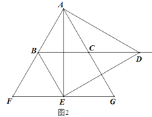
【答案】(1)①证明见解析;②证明见解析;(2)四边形BCGE是菱形,理由见解析.
【解析】
(1)①利用有两条边对应相等并且夹角相等的两个三角形全等即可证明△AEB≌△ADC;
②由△AEB≌△ADC,可得∠ABE=∠C=60°,进而证明∠ABE=∠BAC,则可得到EB∥GC又EG∥BC,所以四边形BCGE是平行四边形;
(2)与(1)一样可证得△ABE≌△ADC,得到BE=CD;与(1)一样可证得四边形BCGE为平行四边形,根据菱形的判定方当BC=BE时,四边形BCGE是菱形,此时BC=CD,所以有DC=BC时,四边形BCGE是菱形.
解:(1)证明:
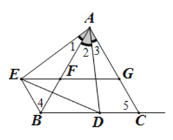
∵△ABC与△ADE都是等边三角形
∴AE=AD,AB=AC,∠EAD=∠BAC=60
∴∠1+∠2=∠2+∠3=60
即∠1=∠3
∴△AEB≌△ADC
②由①可得△AEB≌△ADC,△ABC是等边三角形
∴∠4=∠5=∠BAC=60
∴BE∥CG
∵EG∥BC
∴四边形BCGE是平行四边形
(2)四边形BCGE是菱形,理由是:

由(1)同理可得△AEB≌△ADC
∴∠ABE=∠6=180-∠7=180-60=120,BE=CD
∴∠ABE+∠BAC=120+60=180,∴BE∥AG
∵EG∥BC
∴四边形BCGE是平行四边形
∵CD=BC,∴BE=BC
∴四边形BCGE是菱形