题目内容
过三角形的重心任作一直线,把这个三角形分成两部分,求证:这两部分面积之差不大于整个三角形面积的
.
| 1 |
| 9 |
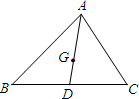
设△ABC重心为G,过点G分别作各边的平行线与各边交点依次为A1、B1、B2、C1、C2、A2
连接A1A2;B1B2、C1C2,
∵三角形重心到一个顶点的距离等于它到对边中点距离的二倍,
∴A1A=A1Bl=B1B,BB2=B2Cl=C1C,CC2=C2A2=A2A,
∵A1A2∥BC,B1B2∥AC,C1C2∥AB,
∴图中的9个三角形全等.
即△AA1A2≌△A1B1G≌△B2GB1≌△C2ClC、
所以上述9个小三角形的面积均等于△ABC面积的
.
若过点C作的直线恰好与直线A1C1、B1C2、B2A2重合,则△ABC被分成的两部分的面积之差等于一个小三角形的面积,即等于△ABC面积的
.
若过点C作的直线不与直线A1C1、B1C2、B2A2重合,不失一般性,设此直线交AC于F,交AB于E,交C1C2于D,
∵GBl=GC2,∠EB1G=∠DC2C,∠B1GE=∠C2GD,
∴△B1GE≌△C2GD、
∴EF分△ABC成两部分的面积之差等于|S△C2DF-S四边形DFCC1|,
而这个差的绝对值不会超过S△C1C2C的面积.
从而EF分△ABC成两部分的面积之差不大于△ABC面积的
.
综上所述:过三角形重心的任一直线分三角形成两部分的面积之差不大于整个三角形面积的
.
连接A1A2;B1B2、C1C2,
∵三角形重心到一个顶点的距离等于它到对边中点距离的二倍,
∴A1A=A1Bl=B1B,BB2=B2Cl=C1C,CC2=C2A2=A2A,
∵A1A2∥BC,B1B2∥AC,C1C2∥AB,
∴图中的9个三角形全等.
即△AA1A2≌△A1B1G≌△B2GB1≌△C2ClC、
所以上述9个小三角形的面积均等于△ABC面积的
| 1 |
| 9 |
若过点C作的直线恰好与直线A1C1、B1C2、B2A2重合,则△ABC被分成的两部分的面积之差等于一个小三角形的面积,即等于△ABC面积的
| 1 |
| 9 |
若过点C作的直线不与直线A1C1、B1C2、B2A2重合,不失一般性,设此直线交AC于F,交AB于E,交C1C2于D,
∵GBl=GC2,∠EB1G=∠DC2C,∠B1GE=∠C2GD,
∴△B1GE≌△C2GD、
∴EF分△ABC成两部分的面积之差等于|S△C2DF-S四边形DFCC1|,
而这个差的绝对值不会超过S△C1C2C的面积.
从而EF分△ABC成两部分的面积之差不大于△ABC面积的
| 1 |
| 9 |
综上所述:过三角形重心的任一直线分三角形成两部分的面积之差不大于整个三角形面积的
| 1 |
| 9 |


练习册系列答案
相关题目