题目内容
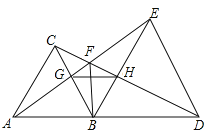
【题目】如图,四边形ABCD是矩形,对角线AC的垂直平分线EF交AC于O,分别交BC、AD于点E、F.
(1)求证:四边形AECF是菱形;
(2)若AB=4,BC=8,求EC的长.

【答案】(1)证明见解析;(2)5.
【解析】
(1)根据EF是AC的垂直平分线,四边形ABCD是矩形,可得OA=OC,∠AOF=∠COE=90°,AD∥BC,∠FAO=∠ECO,利用ASA可证![]() ,可得四边形AECF是平行四边形,根据EF⊥AC,得到平行四边形AECF是菱形;
,可得四边形AECF是平行四边形,根据EF⊥AC,得到平行四边形AECF是菱形;
(2)根据勾股定理可求菱形的边长.
(1)证明:∵EF是AC的垂直平分线,
∴OA=OC,∠AOF=∠COE=90°
∵四边形ABCD是矩形,∴AD∥BC,∴∠FAO=∠ECO
在![]() 和
和![]() 中
中
∠FAO=∠ECO,OA=OC,∠AOF=∠COE,
∴![]() (ASA),
(ASA),
∴OF=OE
又∵OA=OC,
∴四边形AECF是平行四边形
又∵EF⊥AC,
∴平行四边形AECF是菱形
(2)设EC=x,
∵四边形AECF是菱形,则:AE=CE=x, BE=8-x
在![]() 中,由勾股定理得
中,由勾股定理得
![]() ,
,
∴![]()
解得:![]()
即EC=5

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案【题目】用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为![]() ,它各边上格点的个数之和为
,它各边上格点的个数之和为![]() .
.

探究一:图中①—④的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数之和的对应关系如表:
多边形的序号 | ① | ② | ③ | ④ | … |
多边形的面积 | 2 | 2.5 | 3 | 4 | … |
各边上格点的个数和 | 4 | 5 | 6 | 8 | … |
![]() 与
与![]() 之间的关系式为:________.
之间的关系式为:________.
探究二:图中⑤—⑧的格点多边形内部都只有2个格点,请你先完善下表格的空格部分(即分别计算出对应格点多边形的面积![]() ):
):
多边形的序号 | ⑤ | ⑥ | ⑦ | ⑧ | … |
多边形的面积 | … | ||||
各边上格点的个数和 | 4 | 5 | 6 | 8 | … |
![]() 与
与![]() 之间的关系式为:________.
之间的关系式为:________.
猜想:当格点多边形内部有且只有![]() 个格点时,
个格点时,![]() 与
与![]() 之间的关系式为:_______.
之间的关系式为:_______.
【题目】“保护环境,人人有责”,为了更好的治理好金水河,郑州市污水处理厂决定购买![]() 、
、![]() 两型号污水处理设备共10台,其信息如下表:
两型号污水处理设备共10台,其信息如下表:
单价(万元/台) | 每台处理污水量(吨/月) | |
| 12 | 220 |
| 10 | 200 |
(1)设购买![]() 设备
设备![]() 台,所需资金共为W万元,每月处理污水总量为y吨,试写出W与
台,所需资金共为W万元,每月处理污水总量为y吨,试写出W与![]() ,
,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)经预算,市污水处理厂购买设备的资金不超过106万元,月处理污水量不低于2040吨,请你列举出所有购买方案,并指出哪种方案更省钱,需要多少资金?