题目内容
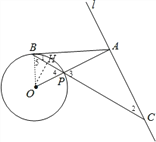
【题目】如图,已知直线![]() 与⊙O相离,OA⊥
与⊙O相离,OA⊥![]() 于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线
于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线![]() 于点C,使得AB=AC.
于点C,使得AB=AC.

(1)求证:AB是⊙O的切线;
(2)若PC=2![]() ,OA=4,求⊙O的半径.
,OA=4,求⊙O的半径.
【答案】(1)详见解析;(2)1.
【解析】试题分析:(1)连结OB,如图,由等腰三角形的性质得∠1=∠2,∠4=∠5,由OA⊥AC得∠2+∠3=90°,加上∠3=∠4,易得∠5+∠1=90°,即∠OBA=90°,于是根据切线的判定定理可得AB是⊙O的切线;
(2)作OH⊥PB于H,如图,根据垂径定理得到BH=PH,设⊙O的半径为r,则PA=OA-OP=4-r,根据勾股定理得到AC,AB,然后根据相似三角形的性质即可得到结论.
(1)证明:连结OB,
∵AB=AC,
∴∠1=∠2,
∵OA⊥AC,
∴∠2+∠3=90°,
∵OB=OP,
∴∠4=∠5,而∠3=∠4,
∴∠5+∠2=90°,
∴∠5+∠1=90°,即∠OBA=90°,
∴OB⊥AB,
∴AB是⊙O的切线;
(2)解:设⊙O的半径为r,则PA=OA﹣OP=4﹣r,
在Rt△PAC中,AC2=PC2﹣PA2=(2![]() )2﹣(4﹣r)2,
)2﹣(4﹣r)2,
在Rt△OAB中,AB2=OA2﹣OB2=42﹣r2,而AB=AC,
∴(2![]() 2﹣(4﹣r)2=42﹣r2,
2﹣(4﹣r)2=42﹣r2,
解得r=1,
即⊙O的半径为1.

【题目】疫情期间福州一中初中部举行了“宅家运动会”.该学校七、八年级各有300名学生参加了这次“宅家运动会”,现从七、八年级各随机抽取20名学生宅家运动会的成绩进行抽样调查.
收集数据如下:
七年级: | 74 | 97 | 96 | 72 | 98 | 99 | 72 | 73 | 76 | 74 |
74 | 69 | 76 | 89 | 78 | 74 | 99 | 97 | 98 | 99 | |
八年级: | 76 | 88 | 96 | 89 | 78 | 94 | 89 | 94 | 95 | 50 |
89 | 68 | 65 | 89 | 77 | 86 | 89 | 88 | 92 | 91 |
整理数据如下:
|
|
|
|
| |
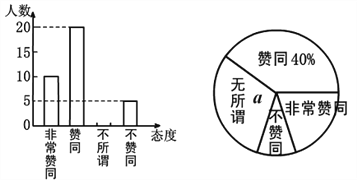
七年级 | 0 | 1 | 10 | 1 | a |
八年级 | 1 | 2 | 3 | 8 | 6 |
分析数据如下:
年级 | 平均数 | 中位数 | 众数 | 方差 |
七年级 | 84.2 | 77 | 74 | 138.56 |
八年级 | 84 | b | 89 | 129.7 |
根据以上信息,回答下列问题:
(1)![]() ___________,
___________,![]() ___________;
___________;
(2)你认为哪个年级“宅家运动会”的总体成绩较好,说明理由(至少从两个不同的角度说明推断的合理性)
(3)学校对“宅家运动会”成绩不低于80分的学生颁发优胜奖,请你估计学校七、八年级所有学生中获得优胜奖的大约有___________人.
【题目】世界上大部分国家都使用摄氏温度(![]() ),但美国、英国等国家的天气预报仍然使用华氏温度(
),但美国、英国等国家的天气预报仍然使用华氏温度(![]() ).两种计量之间有如下对应:
).两种计量之间有如下对应:
摄氏温度( |
|
|
|
|
|
|
华氏温度( |
|
|
|
|
|
|
(1)上表反映了哪两变量之间的关系?哪个是自变量?哪个是因变量?
(2)由上表可得:摄氏温度(![]() )每提高
)每提高![]() 度,华氏温度(
度,华氏温度(![]() )提高_____度.
)提高_____度.
(3)摄氏温度![]() 度时华氏温度为______度.
度时华氏温度为______度.
(4)华氏温度![]() 度时摄氏温度为_______度.
度时摄氏温度为_______度.
(5)华氏温度的值与对应的摄氏温度的值有相等的可能吗?如果有,求出这个值.如果没有,请说明理由.