题目内容
【题目】已知整数a1，a2，a3，a4，┈满足下列条件;a1=0,a2=-|a1+1|,a3=-|a2+2|，a4=-|a3+3|，┈，依次类推，则a2012 的值为（ ）
A.-2012B.-1005C.-1006D.-1007
【答案】C
【解析】
根据条件求出前几个数的值，再分n是奇数时，结果等于-
，n是偶数时，结果等于-
，然后把n的值代入进行计算即可得解．
a1=0，
a2=-|a1+1|=-|0+1|=-1，
a3=-|a2+2|=-|-1+2|=-1，
a4=-|a3+3|=-|-1+3|=-2，
a5=-|a4+4|=-|-2+4|=-2，
…，
所以，n是奇数时，an=-，n是偶数时，an=-，
a2012=-
=-1006．
故选C．
小学教材全测系列答案
【题目】在⊙O中，直径AB＝6，BC是弦，∠ABC＝30°，点P在BC上，点Q在⊙O上，且OP⊥PQ．
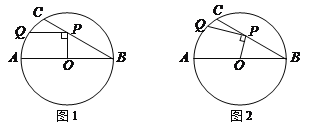
（1）如图1，当PQ∥AB时，求PQ的长度；
（2）如图2，当点P在BC上移动时，求PQ长的最大值．
【题目】某商场计划用3 800元购进节能灯120只，这两种节能灯的进价、售价如下表：
进价(元/只) | 售价(元/只) | |
甲型 | 25 | 30 |
乙型 | 45 | 60 |
(1)求甲、乙两种节能灯各进多少只？
(2)全部售完120只节能灯后，该商场获利润多少元？
【题目】某商场柜台销售每台进价分别为160元、120元的
、
两种型号的电器，下表是近两周的销售情况：
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
（进价、售价均保持不变，利润＝销售收入—进货成本）
（1）求、两种型号的电器的销售单价；
（2）若商场准备用不多于7500元的金额再采购这两种型号的电器共50台，求种型号的电器最多能采购多少台？
（3）在（2）中商场用不多于7500元采购这两种型号的电器共50台的条件下，商场销售完这50台电器能否实现利润超过1850元的目标？若能，请给出相应的采购方案；若不能，请说明理由.
