题目内容
如图,反比例函数y= 的图象过矩形OABC的顶点B,OA、0C分别在x轴、y轴的正半轴上,OA:0C=2:1.
的图象过矩形OABC的顶点B,OA、0C分别在x轴、y轴的正半轴上,OA:0C=2:1.

(1)求B点的坐标;
(2)若直线y=2x+m平分矩形OABC面积,求m的值.
 的图象过矩形OABC的顶点B,OA、0C分别在x轴、y轴的正半轴上,OA:0C=2:1.
的图象过矩形OABC的顶点B,OA、0C分别在x轴、y轴的正半轴上,OA:0C=2:1.
(1)求B点的坐标;
(2)若直线y=2x+m平分矩形OABC面积,求m的值.
(1)B(4,2) (2)-3
试题分析:(1)设OA=2x,则OC=x,由于点B在反比例函数y=
 的图象上,所以OA•OB=8,进而可得出x的值,求出B点坐标;
的图象上,所以OA•OB=8,进而可得出x的值,求出B点坐标;(2)根据直线y=2x+m平分矩形OABC面积可知此直线必过矩形两对角线的交点,把矩形对角线的交点坐标代入直线y=2x+m即可求出m的值.
解:(1)∵OA:0C=2:1,
∴OA=2x,则OC=x,
∵点B在反比例函数y=
 的图象上,
的图象上,∴2x•x=8,
∴x=2,
∴2x=4,
∴B(4,2);
(2)∵四边形OABC是矩形,OA=4,OC=2,
∴A(4,0),C(0,2)
设矩形OABC的两条对角线交点为E,则E为AC的中点,
∴E(2,1),
∴4+m=1,
∴m=﹣3.
点评:本题考查的是反比例函数的性质及矩形的性质,根据题意得出B点坐标是解答此题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 与y轴交于A点,与反比例函数
与y轴交于A点,与反比例函数 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO= .
. 
 (x>0)图像上的点,在y轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图像上的点,在y轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由. (x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若S△AOB=S△OBF+S△OAE,则b= .
(x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若S△AOB=S△OBF+S△OAE,则b= .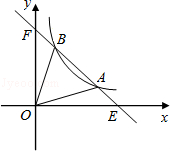

 m3
m3 m3
m3 与直线
与直线 在第二象限内的交点,AB⊥
在第二象限内的交点,AB⊥ 轴于点B,且
轴于点B,且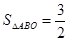 .
.
 的图象交于点P1、P2、P3、P4、P5…,并设△OA1P1、△A1A2P2、△A2A3P3…面积分别为S1、S2、S3…,按此作法进行下去,则Sn的值为 (n为正整数).
的图象交于点P1、P2、P3、P4、P5…,并设△OA1P1、△A1A2P2、△A2A3P3…面积分别为S1、S2、S3…,按此作法进行下去,则Sn的值为 (n为正整数).
 (x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S1+S2+S3+S4+S5的值为( )
(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S1+S2+S3+S4+S5的值为( )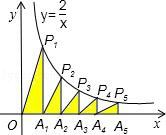
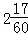

 (x<0)的图象上的一点,过点A作?ABCD,使点B、C在x轴上,点D在y轴上,则?ABCD的面积为( )
(x<0)的图象上的一点,过点A作?ABCD,使点B、C在x轴上,点D在y轴上,则?ABCD的面积为( )
 在同一直角坐标系中的图象大致如图,则下列结论正确的是( )
在同一直角坐标系中的图象大致如图,则下列结论正确的是( )