题目内容
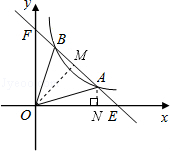
如图,直线y=﹣x+b与双曲线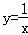 (x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若S△AOB=S△OBF+S△OAE,则b= .
(x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若S△AOB=S△OBF+S△OAE,则b= .
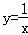 (x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若S△AOB=S△OBF+S△OAE,则b= .
(x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若S△AOB=S△OBF+S△OAE,则b= .
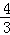
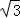
试题分析:根据直线解析式求出点E、F的坐标,过点O作OM⊥AB于点M,设A(x1,y1)、B(x2,y2),联立两函数解析式求解可得y1=x2,y2=x1,从而判断出点A、B关于OM对称,并求出点A的坐标,然后代入双曲线解析式计算即可得解.
解:令y=0,则﹣x+b=0,
解得x=b,
令x=0,则y=b,
所以,点E(b,0)、F(0,b),
所以,OE=OF,
过点O作OM⊥AB于点M,则ME=MF,
设点A(x1,y1)、B(x2,y2),
联立
 ,
,消掉y得,x2﹣bx+1=0,
根据根与系数的关系,x1•x2=1,
所以y1•y2=1,
所以y1=x2,y2=x1,
所以OA=OB,
所以AM=BM(等腰三角形三线合一),
∵S△AOB=S△OBF+S△OAE,
∴FB=BM=AM=AE,
所以点A(
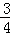 b,
b, b),
b),∵点A在双曲线y=
 上,
上,∴
 b×
b× b=1,
b=1,解得b=

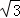 .
.故答案为:

 .
.点评:本题考查了反比例函数与一次函数的交点问题,联立两函数解析式求解得到OA=OB,然后根据三角形的面积求出点A、B、M是线段EF的四等分点,并求出点A的坐标是解题的关键.

练习册系列答案
相关题目
 ,D是AB边上的一点,将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是_________.
,D是AB边上的一点,将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是_________.
 ,OB=4,OE=2.
,OB=4,OE=2.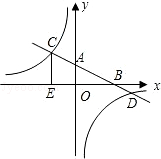
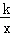 的图象交于点A(3,2)
的图象交于点A(3,2)
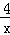 (x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…△PnAn﹣1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…An﹣1An都在x轴上
(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…△PnAn﹣1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…An﹣1An都在x轴上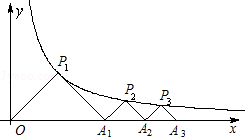
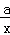 相交于点A(1,b)、点B(c,﹣2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a= .
相交于点A(1,b)、点B(c,﹣2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a= .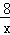 的图象过矩形OABC的顶点B,OA、0C分别在x轴、y轴的正半轴上,OA:0C=2:1.
的图象过矩形OABC的顶点B,OA、0C分别在x轴、y轴的正半轴上,OA:0C=2:1.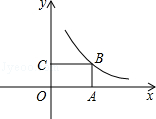
 (k2≠0)的图象的一个交点为(m、n),则另一个交点为 .
(k2≠0)的图象的一个交点为(m、n),则另一个交点为 .