题目内容
如图,点A是反比例函数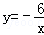 (x<0)的图象上的一点,过点A作?ABCD,使点B、C在x轴上,点D在y轴上,则?ABCD的面积为( )
(x<0)的图象上的一点,过点A作?ABCD,使点B、C在x轴上,点D在y轴上,则?ABCD的面积为( )

A. 1 B. 3 C. 6 D. 12
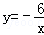 (x<0)的图象上的一点,过点A作?ABCD,使点B、C在x轴上,点D在y轴上,则?ABCD的面积为( )
(x<0)的图象上的一点,过点A作?ABCD,使点B、C在x轴上,点D在y轴上,则?ABCD的面积为( )
A. 1 B. 3 C. 6 D. 12
C
试题分析:过点A作AE⊥OB于点E,则可得?ABCD的面积等于矩形ADOE的面积,继而结合反比例函数的k的几何意义即可得出答案.
解:过点A作AE⊥OB于点E,
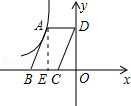
因为矩形ADOE的面积等于AD×AE,平行四边形ABCD的面积等于:AD×AE,
所以?ABCD的面积等于矩形ADOE的面积,
根据反比例函数的k的几何意义可得:矩形ADOC的面积为6,即可得平行四边形ABCD的面积为6.
故选C.
点评:此题考查了反比例函数的k的几何意义及平行四边形的性质,根据题意得出?ABCD的面积等于矩形ADOE的面积是解答本题的关键.

练习册系列答案
相关题目
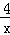 (x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…△PnAn﹣1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…An﹣1An都在x轴上
(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…△PnAn﹣1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…An﹣1An都在x轴上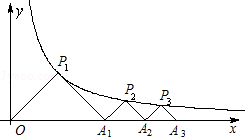
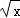 →y=3
→y=3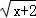 +1;y=3
+1;y=3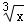 →y=3
→y=3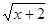 +1;
+1;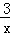 →y=
→y=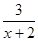 +1;…
+1;… +1图象再往 _________ 平移 _______ 个单位,所得函数图象的解析式为y=
+1图象再往 _________ 平移 _______ 个单位,所得函数图象的解析式为y=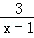 +1;
+1;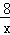 的图象过矩形OABC的顶点B,OA、0C分别在x轴、y轴的正半轴上,OA:0C=2:1.
的图象过矩形OABC的顶点B,OA、0C分别在x轴、y轴的正半轴上,OA:0C=2:1.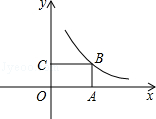
 交于点A,B.过点A作AM⊥x轴,垂足为点M,连接BM.若S△ABM=1,则k的值是( )
交于点A,B.过点A作AM⊥x轴,垂足为点M,连接BM.若S△ABM=1,则k的值是( )
 的图象如图,当x≥﹣1时,y的取值范围是( )
的图象如图,当x≥﹣1时,y的取值范围是( )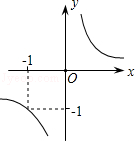
 (k2≠0)的图象的一个交点为(m、n),则另一个交点为 .
(k2≠0)的图象的一个交点为(m、n),则另一个交点为 .