题目内容
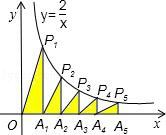
如图，在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5，过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数
（x≠0）的图象相交于点P1、P2、P3、P4、P5，得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5，并设其面积分别为S1、S2、S3、S4、S5，则S1+S2+S3+S4+S5的值为（ ）
（x≠0）的图象相交于点P1、P2、P3、P4、P5，得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5，并设其面积分别为S1、S2、S3、S4、S5，则S1+S2+S3+S4+S5的值为（ ）| A．2 | B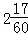． | C．3 | D． |
B
试题分析：由于过双曲线上的任意一点分别向两条坐标轴作垂线，与坐标轴围成的矩形面积就等于|k|，可先由|k|依次表示出图中各阴影三角形的面积，再相加即可得到面积的和．
解：由于OA1=A1A2=A2A3=A3A4=A4A5，S1=
|k|，S2=
|k|，S3=
|k|，S4=
|k|，S5=
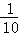|k|；则S1+S2+S3+S4+S5=（
+
+
+
+
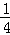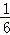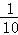）|k|=
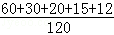×2=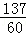
=
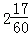．故选B．
点评：本题灵活考查了反比例函数系数k的几何意义，过双曲线上的任意一点分别向两条坐标轴作垂线，与坐标轴围成的矩形面积就等于|k|．
练习册系列答案
相关题目
是反比例函数？
相交于点A（1，b）、点B（c，﹣2），求k+a的值．甲同学说：未知数太多，很难求的；乙同学说：可能不是用待定系数法来求；丙说：如果用数形结合的方法，利用两交点在坐标系中位置的特殊性，可以试试．请结合他们的讨论求出k+a= ．
（x＞0）的图象分别交于点A1、A2、A3、A4、…；与函数y=
的图象分别交于点B1、B2、B3、B4、…．如果四边形A1A2B2B1的面积记为S1，四边形A2A3B3B2的面积记为S2，四边形A3A4B4B3的面积记为S3，…，以此类推．则S10的值是（ ）
的图象过矩形OABC的顶点B，OA、0C分别在x轴、y轴的正半轴上，OA：0C=2：1．
交OB于D，且OD：DB=1：2，若△OBC的面积等于3，则k的值（ ）
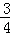
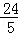
的图象如图，当x≥﹣1时，y的取值范围是（ ）
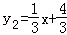．当y1＞y2时，x的范围是（ ）
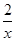的图象经过点A(m，1)，则m的值为 ．