题目内容
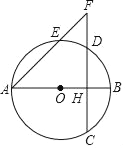
【题目】如图，AC是⊙O的直径，点B，D在⊙O上，点E在⊙O外，∠EAB=∠D=30°．
（1）∠C的度数为 ；
（2）求证：AE是⊙O的切线；
（3）当AB=3时，求图中阴影部分的面积（结果保留根号和π）．
【答案】（1）∠C=30°；（2）证明见解析；（3）
+3π．
【解析】
（1）直接根据圆周角定理得到∠C=∠D=30°；
（2）先根据圆周角定理得∠ABC=90°，则∠BAC=60°，所以∠EAC=∠EAB+∠BAC=90°，于是可根据切线的判定定理得到AE是⊙O的切线；
（3）连结OB，先判断△OAB为等边三角形，则OA=3，∠AOB=60°，所以∠BOC=120°，然后利用图中阴影部分的面积=S△AOB+S扇形BOC和扇形的面积公式、等边三角形的面积公式计算即可．
（1）∠C=∠D=30°．
故答案为：30°；
（2）∵AC是⊙O的直径，∴∠ABC=90°，∴∠BAC=60°，而∠EAB=30°，∴∠EAC=∠EAB+∠BAC=90°，∴CA⊥AE，∴AE是⊙O的切线；
（3）连结OB，如图，∵∠BAC=60°，AB=3，∴△OAB为等边三角形，∴OA=3，∠AOB=60°，∴∠BOC=120°，∴图中阴影部分的面积=S△AOB+S扇形BOC=
×32+
=+3π．
【题目】学校在八年级新生中举行了全员参加的数学应用能力大赛，试卷题目共10题，每题10分.现分别从三个班中各随机取10名同学的成绩（单位：分），收集数据如下：
1班：90，70，80，80，80，80，80，90，80，100；
2班：70，80，80，80，60，90，90，90，100，90；
3班：90，60，70，80，80，80，80，90，100，100.
整理数据：
人数 班级 | 60分人数 | 70分人数 | 80分人数 | 90分人数 | 100分人数 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
平均数 | 中位数 | 众数 | |
83 | 80 | 80 | |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
分析数据：
根据以上信息回答下列问题：
（1）请直接写出表格中
，
，
，
的值；
（2）比较这三组样本数据的平均数、中位数和众数，你认为哪个班的成绩比较好？请说明理由（写两条支持你结论的理由）.
