题目内容
【题目】连接多边形任意两个不相邻顶点的线段称为多边形的对角线.
(1)
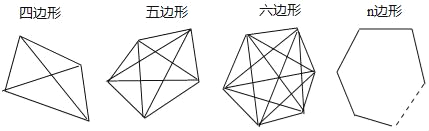
对角线条数分别为 、 、 、 .
(2)n边形可以有20条对角线吗?如果可以,求边数n的值;如果不可以,请说明理由.
(3)若一个n边形的内角和为1800°,求它对角线的条数.
【答案】(1)2;5;9;![]() ;(2)n边形可以有20条对角线,此时边数n为八;(3)这个多边形有54条对角线
;(2)n边形可以有20条对角线,此时边数n为八;(3)这个多边形有54条对角线
【解析】分析:(1)设n边形的对角线条数为an,根据多边形对角线条数公式即可求出结论;
(2)假设可以,根据多边形对角线条数公式,可得出关于n的一元二次方程,解之即可得出结论;
(3)根据多边形内角和定理,可求出边数,再套用多边形对角线条数公式,即可得出结论.
详解:(1)设n边形的对角线条数为an,
则a4=![]() =2,a5=
=2,a5=![]() =5,a6=
=5,a6=![]() =9,…,an=
=9,…,an=![]() .
.
(2)假设可以,根据题意得:
![]() =20,
=20,
解得:n=8或n=-5(舍去),
∴n边形可以有20条对角线,此时边数n为八.
(3)∵一个n边形的内角和为1800°,
∴180°×(n-2)=1800°,
解得:n=12,
∴![]() =
=![]() =54.
=54.
答:这个多边形有54条对角线.

练习册系列答案
相关题目