题目内容
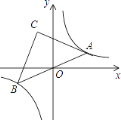
【题目】如图，菱形ABCD边长为5，顶点A，B在x轴的正半轴上，顶点D在y轴的正半轴上，且点A的坐标是（3，0），以点C为顶点的抛物线经过点A．
（1）求点C的坐标；
（2）求抛物线的解析式；
（3）若将上述抛物线进行平移，使得平移后的抛物线的顶点P在直线BC上，且此时的抛物线恰好经过点D，求平移后的抛物线解析式及其顶点P的坐标．
【答案】（1）点C（5，4）；（2）y＝﹣（x﹣5）2+4；（3）y＝﹣（x﹣2）2﹣8或y＝﹣（x+
）2+24，点P（2，﹣8）或（﹣，24）.
【解析】
（1）OA=3，AD=5，则DO=4，故点D（0，4），点C（5，4）；
（2）抛物线的表达式为：y=a（x-5）2+4，将点A的坐标代入上式并解得：a=-1，即可求解；
（3）直线BC的表达式为：
；设点P的坐标为：（m，
），而点D（0，4），则抛物线的表达式为：y=-（x-m）2，将点D的坐标代入上式并整理得：3m2+4m-20=0，即可求解．
（1）OA＝3，AD＝5，则DO＝4，故点D（0，4），点C（5，4）；
（2）抛物线的表达式为：y＝a（x﹣5）2+4，将点A的坐标代入上式并解得：a＝﹣1，
故抛物线的表达式为：y＝﹣（x﹣5）2+4；
（3）点A的坐标是（3，0），AB＝5，则点B（8，0），将点B、C的坐标代入一次函数表达式y＝kx+b得：
，解得：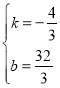
，
故直线BC的表达式为：y＝﹣
x+
；
设点P的坐标为：（m，﹣m+），而点D（0，4），
则抛物线的表达式为：y＝﹣（x﹣m）2﹣m+，
将点D的坐标代入上式并整理得：3m2+4m﹣20＝0，解得：m＝2或﹣，
故点P（2，﹣8）或（﹣，24），
故抛物线的表达式为：y＝﹣（x﹣2）2﹣8或y＝﹣（x+）2+24．
练习册系列答案
阅读快车系列答案
相关题目
