Question

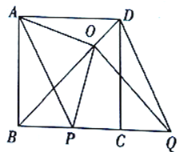
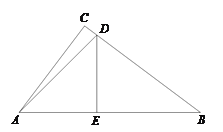
【题目】如图，在Rt△ABC中，，点在边上，⊥，点为垂足，，∠DAB=450，tanB=.

(1)求的长；

(2)求的余弦值．

Answer 1

【答案】(1)3;(2)

【解析】分析：（1）由题意得到三角形ADE为等腰直角三角形，在直角三角形DEB中，利用锐角三角函数定义求出DE与BE之比，设出DE与BE，由AB=7求出各自的值，确定出DE即可；

（2）在直角三角形中，利用勾股定理求出AD与BD的长，根据tanB的值求出cosB的值，确定出BC的长，由BC﹣BD求出CD的长，利用锐角三角函数定义求出所求即可．

详解：（1）∵DE⊥AB，∴∠DEA=90°．又∵∠DAB=45°，∴DE=AE．在Rt△DEB中，∠DEB=90°，tanB==，设DE=3x，那么AE=3x，BE=4x．∵AB=7，∴3x+4x=7，解得：x=1，∴DE=3；

（2）在Rt△ADE中，由勾股定理，得：AD=3，同理得：BD=5．在Rt△ABC中，由tanB=，可得：cosB=，∴BC=，∴CD=，∴cos∠CDA==，即∠CDA的余弦值为．