题目内容
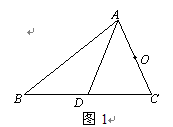
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB="4" .以斜边AB的中点D为旋转中心,把△ABC按逆时针方向旋转 角(
角( ),当点A的对应点与点C重合时,B,C两点的对应点分别记为E,F,EF与AB的交点为G,此时
),当点A的对应点与点C重合时,B,C两点的对应点分别记为E,F,EF与AB的交点为G,此时 等于 ° ,△DEG的面积为 .
等于 ° ,△DEG的面积为 .
 角(
角( ),当点A的对应点与点C重合时,B,C两点的对应点分别记为E,F,EF与AB的交点为G,此时
),当点A的对应点与点C重合时,B,C两点的对应点分别记为E,F,EF与AB的交点为G,此时 等于 ° ,△DEG的面积为 .
等于 ° ,△DEG的面积为 .
60,

根据直角三角形性质求出AC,∠A,根据旋转性质求出DA=DC,得出等边三角形ADC,求出∠EDG=60°和DC,求出ED长,求出∠DGE=90°,求出DG和EG,根据三角形的面积公式求出即可.
解:∵∠ACB=90°,∠B=30°,
∴∠A=60°,AC= AB=2,
AB=2,
∵以斜边AB的中点D为旋转中心,点A的对应点与点C重合,
∴DA=DC,
∴∠A=∠ACD=60°,
∴△ADC是等边三角形,
AC=AD=DC=2,∠ADC=60°=∠EDG,
∴DE=CE-CD=4-2=2,∠DGE=90°,
∵∠E=30°,
∴DG= DE=1,
DE=1,
由勾股定理得:GE= ,
,
∴S△DEG= DG×GE=
DG×GE= ×1×
×1× =
= .
.
故答案为:60, .
.
解:∵∠ACB=90°,∠B=30°,
∴∠A=60°,AC=
 AB=2,
AB=2,∵以斜边AB的中点D为旋转中心,点A的对应点与点C重合,
∴DA=DC,
∴∠A=∠ACD=60°,
∴△ADC是等边三角形,
AC=AD=DC=2,∠ADC=60°=∠EDG,
∴DE=CE-CD=4-2=2,∠DGE=90°,
∵∠E=30°,
∴DG=
 DE=1,
DE=1,由勾股定理得:GE=
 ,
,∴S△DEG=
 DG×GE=
DG×GE= ×1×
×1× =
= .
.故答案为:60,
 .
.
练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目


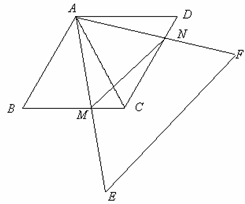


 ,∠C=30
,∠C=30 B 2
B 2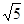 C 4
C 4 D 4
D 4