题目内容
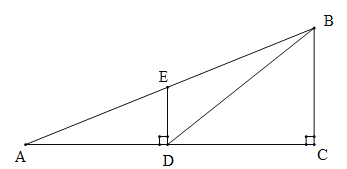
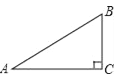
【题目】某校计划把一块近似于直角三角形的废地开发为生物园,如图所示,∠ACB=90°,BC=60米,∠A=36°.
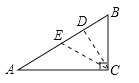
(1)若入口处E在AB边上,且与A、B等距离,求CE的长(精确到个位);
(2)若D点在AB边上,计划沿线段CD修一条水渠.已知水渠的造价为50元/米,水渠路线应如何设计才能使造价最低,求出最低造价.
(其中sin36°=0.5878,cos36°=0.8090,tan36°=0.7265)
【答案】(1)51;(2)2427元.
【解析】试题分析:(1)根据已知求得AB的长,再根据斜边上的中线等于斜边的一半从而求得CE的长;
(2)过C作CD⊥AB,则沿线段CD修水渠造价最低.
试题解析:解:(1)在Rt△ABC中,AB=![]() =
=![]() =102.08.又∵CE是Rt△ABC中斜边AB上的中线,∴CE=
=102.08.又∵CE是Rt△ABC中斜边AB上的中线,∴CE=![]() AB≈51(米).
AB≈51(米).
(2)在Rt△ABC中作CD⊥AB交AB于D点,则沿线段CD修水渠造价最低,∴∠DCB=∠A=36°,∴在Rt△BDC中,CD=BC×cos∠DCB=60×cos36°=48.54,∴水渠的最低造价为:50×48.54=2427(元).
答:水渠的最低造价为2427元.

练习册系列答案
相关题目