ЬтФПФкШн
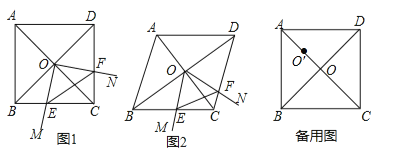
ЁОЬтФПЁПЃЈБОЬтТњЗж6ЗжЃЉШчЭМЃЌЙлВтЕуAЁЂЦьИЫDEЕФЕзЖЫDЁЂФГТЅЗПCBЕФЕзЖЫCШ§ЕудквЛЬѕжБЯпЩЯЃЌДгЕуAДІВтЕУТЅЖЅЖЫBЕФбіНЧЮЊ22ЁуЃЌДЫЪБЕуEЧЁКУдкABЩЯЃЌДгЕуDДІВтЕУТЅЖЅЖЫBЕФбіНЧЮЊ38ЃЎ5ЁуЃЎвбжЊЦьИЫDEЕФИпЖШЮЊ12УзЃЌЪдЧѓТЅЗПCBЕФИпЖШЃЎ
ЃЈВЮПМЪ§ОнЃКsin22ЁуЁж0ЃЎ37ЃЌcos22ЁуЁж0ЃЎ93ЃЌtan22ЁуЁж0ЃЎ40ЃЌsin38ЃЎ5ЁуЁж0ЃЎ62ЃЌcos38ЃЎ5ЁуЁж0ЃЎ78ЃЌtan38ЃЎ5ЁуЁж0ЃЎ80ЃЉ
ЁОД№АИЁП24Уз
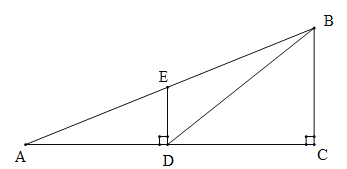
ЁОНтЮіЁПЪдЬтЗжЮіЃКЙЙдьжБНЧШ§НЧаЮЃЌРћгУШёНЧШ§НЧКЏЪ§РДНтжБНЧШ§НЧаЮЕФЮЪЬтЃЌДгЖјНтОіЪЕМЪЮЪЬтЃЎ
ЪдЬтНтЮіЃКНтЗЈвЛЃКШчЭМЃЌЙ§ЕуEзїEFЁЭBCЃЌФЧУДCF=DE=12ЃЌEF=DCC,
ЩшBC=xЃЌФЧУД![]()
МД![]()
НтЕУx=24
ЫљвдТЅЗПCBЕФИпЖШЮЊ24УзЃЎ
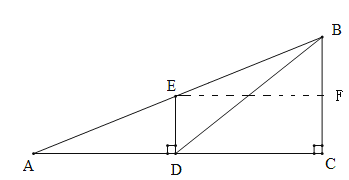
НтЗЈЖўЃКдкRtЁїADEжаЃЌtanA=![]() ЃЌМДAD=
ЃЌМДAD=![]()
дкRtЁїACBжаЃЌAC=![]()
дкRtЁїDCBжаЃЌDC=![]()
Ыљвд![]()
НтЕУBC=24
ЫљвдТЅЗПCBЕФИпЖШЮЊ24УзЃЎ

ЁОЬтФПЁПФГЧјОйааЁАжаЛЊЫа![]() ОЕфЫаЖСЁБДѓШќЃЌаЁбЇЁЂжабЇзщИљОнГѕШќГЩМЈЃЌИїбЁГі5УћбЁЪжзщГЩаЁбЇДњБэЖгКЭжабЇДњБэЖгВЮМгЪаМЖОіШќЃЌСНИіДњБэЖгИїбЁГіЕФ5УћбЁЪжЕФОіШќГЩМЈЗжБ№ЛцжЦГЩЯТСаСНИіЭГМЦЭМ
ОЕфЫаЖСЁБДѓШќЃЌаЁбЇЁЂжабЇзщИљОнГѕШќГЩМЈЃЌИїбЁГі5УћбЁЪжзщГЩаЁбЇДњБэЖгКЭжабЇДњБэЖгВЮМгЪаМЖОіШќЃЌСНИіДњБэЖгИїбЁГіЕФ5УћбЁЪжЕФОіШќГЩМЈЗжБ№ЛцжЦГЩЯТСаСНИіЭГМЦЭМ

ИљОнвдЩЯаХЯЂЃЌећРэЗжЮіЪ§ОнШчЯТЃК
ЦНОљЪ§ЃЈЗж | жаЮЛЪ§ЃЈЗж | жкЪ§ЃЈЗж | |
аЁбЇзщ | 85 |
| 100 |
жабЇзщ |
| 85 |
|
ЃЈ1ЃЉаДГіБэИёжа![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФжЕЃК
ЕФжЕЃК![]() ЁЁЁЁЃЌ
ЁЁЁЁЃЌ![]() ЁЁЁЁЃЌ
ЁЁЁЁЃЌ![]() ЁЁЁЁЃЎ
ЁЁЁЁЃЎ
ЃЈ2ЃЉНсКЯСНЖгГЩМЈЕФЦНОљЪ§КЭжаЮЛЪ§НјааЗжЮіЃЌФФИіЖгЕФОіШќГЩМЈНЯКУЃП
ЃЈ3ЃЉМЦЫуСНЖгОіШќГЩМЈЕФЗНВюЃЌВЂХаЖЯФФвЛИіДњБэЖгбЁЪжГЩМЈНЯЮШЖЈЃЎ