题目内容
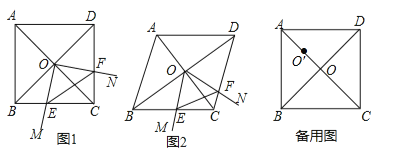
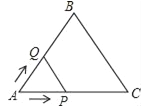
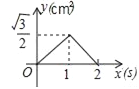
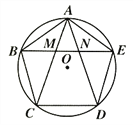
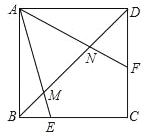
【题目】如图，正方形ABCD中，∠EAF=45°，连接对角线BD交AE于M，交AF于N，若DN=1，BM=2，那么MN=_____．证明：DN2+BM2=MN2．
【答案】
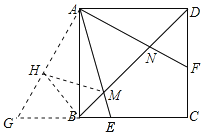
【解析】解：如图，延长CB到G，使BG=DF，连接AG，在AG截取AH=AN，连接MH、BH．∵四边形ABCD为正方形，∴AB=BC=CD=AD，∠BDC=∠ABD=45°，∠BAD=∠ADF=∠ABE=∠ABG=90°．在△ABG和△ADF中，
，∴△ABG≌△ADF（SAS），∴∠BAG=∠DAF，∠AFD=∠G，AF=AG，∴∠GAE=∠BAG+∠BAE=∠DAF+∠BAE=∠BAD﹣∠EAF=90°﹣45°=45°=∠EAF．在△AMN和△AMH中，
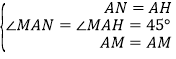，∴△AMN≌△AMH（SAS），∴MN=MH．∵AF=AG，AN=AH，∴FN=AF﹣AN=AG﹣AH=GH．在△DFN和△BGH中，
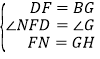，∴△DFN≌△BGH（SAS），∴∠GBH=∠NDF=45°，DN=BH，∴∠MBH=∠ABH+∠ABD=∠ABG﹣∠GBH+∠ABD=90°﹣45°+45°=90°，∴BM2+DN2=BM2+BH2=MH2=MN2．
当DN=1，BM=2时，12+22=MN2，∴MN=
．∵MN＞0，∴MN=．
故答案为：．
练习册系列答案
相关题目
