题目内容
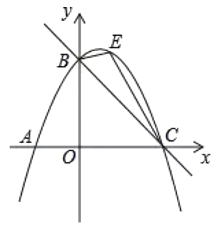
【题目】如图,直线![]() 与 x 轴交于点 C,与 y 轴交于点 B,抛物线
与 x 轴交于点 C,与 y 轴交于点 B,抛物线 ![]() 经过 B、C 两点.
经过 B、C 两点.
(1)求抛物线的解析式;
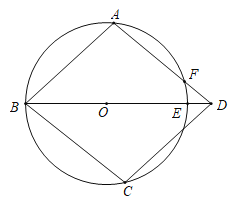
(2)如图,点 E 是抛物线上的一动点(不与 B,C 两点重合),△BEC 面积记为 S,当 S 取何值时,对应的点 E 有且只有三个?
【答案】(1)![]() ;(2)3
;(2)3
【解析】
(1)先利用一次函数解析式确定B(0,3),C(4,0),然后利用待定系数法求抛物线解析式;
(2)由于E点在直线BC的下方的抛物线上时,存在两个对应的E点满足△BEC面积为S,则当E点在直线BC的上方的抛物线上时,只能有一个对应的E点满足△BEC面积为S,所以过E点的直线与抛物线只有一个公共点,设此时直线解析式为![]() ,利用方程组
,利用方程组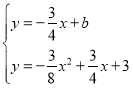 只有一组解求出b得到E点坐标,然后计算此时S△BEC.
只有一组解求出b得到E点坐标,然后计算此时S△BEC.
(1)当x=0时,y=-![]() x+3=3,则B(0,3),
x+3=3,则B(0,3),
当y=0时,-![]() x+3=0,解得x=4,则C(4,0),
x+3=0,解得x=4,则C(4,0),
把B(0,3),C(4,0)代入y=ax2+![]() x+c得
x+c得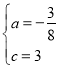 ,
,
所以抛物线解析式为![]() ;
;
(2)当E点在直线BC的下方的抛物线上时,一定有两个对应的E点满足△BEC面积为S,
所以当E点在直线BC的上方的抛物线上时,只能有一个对应的E点满足△BEC面积为S,
即此时过E点的直线与抛物线只有一个公共点,
设此时直线解析式为![]() ,
,
方程组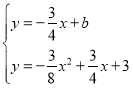 只有一组解,
只有一组解,
方程![]() 有两个相等的实数解,
有两个相等的实数解,
则△=122-4×3×(-24+8b)=0,解得b=![]() ,解方程得x1=x2=2,
,解方程得x1=x2=2,
E点坐标为(2,3),
此时![]() ,
,
所以当S=1时,对应的点E有且只有三个.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
类别 |
|
|
|
|
|
类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 11 | 20 | 40 |
| 4 |
请你根据以上信息,回答下列问题:
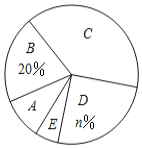
(1)统计表中![]() 的值为_______,统计图中
的值为_______,统计图中![]() 的值为______,
的值为______,![]() 类对应扇形的圆心角为_____度;
类对应扇形的圆心角为_____度;
(2)该校共有1500名学生,根据调查结果,估计该校最喜爱体育节目的学生人数;
(3)样本数据中最喜爱戏曲节目的有4人,其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演,请用树状图或列表求所选2名同学中有男生的概率.