题目内容
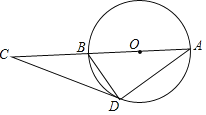
【题目】如图,AB是⊙O的直径,点C是弧AB的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且![]() ,CE的延长线交D的延长线于点F,AF交⊙O于点H,连接BH.
,CE的延长线交D的延长线于点F,AF交⊙O于点H,连接BH.

(1)求证:BD是⊙O的切线;
(2)当OB=2时,求AH的长
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接OC,由垂径定理得出∠AOC=90°,证明OC是△ABD的中位线,得出OC∥BD,由平行线的性质得出∠ABD=∠AOC=90°,即可得出结论;
(2)由平行线得出△OCE∽△BFE,得出![]() =
=![]() =
=![]() ,求出BF=3,由勾股定理得出AF=
,求出BF=3,由勾股定理得出AF=![]() =5,由三角形面积得出BH=
=5,由三角形面积得出BH=![]() =
=![]() ,再由勾股定理即可得出答案.
,再由勾股定理即可得出答案.
解:(1)证明:连接OC,如图所示:
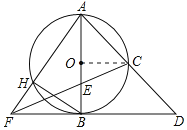
∵AB是⊙O的直径,点C是弧AB的中点,
∴∠AOC=90°,
∵OA=OB,CD=AC,
∴OC是△ABD的中位线,
∴OC∥BD,
∴∠ABD=∠AOC=90°,
∴AB⊥BD,
∴BD是⊙O的切线;
(2)解:由(1)得:OC∥BD,
∴△OCE∽△BFE,
∴![]() =
=![]() =
=![]()
∵OB=2,
∴OC=OB=2,AB=4,
∴![]() =
=![]() ,
,
∴BF=3,
∵∠ABD=90°,
∴∠ABF=90°,
∴AF=![]() =
=![]() =5,
=5,
∵△ABF的面积=![]() AF×BH=
AF×BH=![]() AB×BF,
AB×BF,
∴BH=![]() =
=![]() ,
,
∴AH=![]() =
=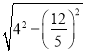 =
=![]() .
.

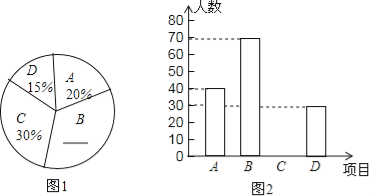
【题目】小明在“五一”假期间参加一项社会调查活动,在他所居住小区的600个家庭中,随机调查了50个家庭人均月收入情况,并绘制了如下的频数分布表和频数分布直方图(收入取整数,单位:元).
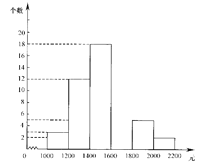
分 组 | 频 数 | 频 率 |
1000~1200 | 3 | 0.060 |
1200~1400 | 12 | 0.240 |
1400~1600 | 18 | 0.360 |
1600~1800 | 0.200 | |
1800~2000 | 5 | |
2000~2200 | 2 | 0.040 |
合计 | 50 | 1.000 |
请你根据以上提供的信息,解答下列问题:
⑴ 补全频数分布表和频数分布直方图;
⑵ 这50个家庭人均月收入的中位数落在 小组;
⑶ 请你估算该小区600个家庭中人均月收入较低(不足1400元)的家庭个数大约有多少?