题目内容
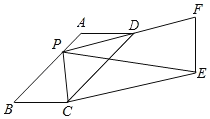
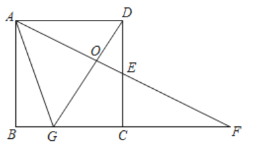
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,
的中点,![]() 和
和![]() 的延长线交于点
的延长线交于点![]() ,点
,点![]() 是边
是边![]() 上的一点,且满足
上的一点,且满足![]() ,连接
,连接![]() ,
,![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() .
.
(1)若![]() ,求
,求![]() 的面积
的面积
(2)当![]() 是直角三角形时,求所有满足要求的
是直角三角形时,求所有满足要求的![]() 值.
值.
(3)记![]() ,
,![]() ,
,
①求![]() 关于
关于![]() 的函数关系.
的函数关系.
②当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)①
;(3)①![]() ;②
;②![]()
【解析】
(1)当a=1时,CG=1,BC=3,GC=2,先由矩形的性质及已知证得![]() ,求出CF=AD=BC=3,再证得
,求出CF=AD=BC=3,再证得![]() 得
得![]() ,然后由等高的面积比等于相似比求得
,然后由等高的面积比等于相似比求得![]() 的面积;
的面积;
(2)分两种情况:①![]() ,②
,②![]() ,利用相似三角形的判定与性质求解即可;
,利用相似三角形的判定与性质求解即可;
(3)①由![]() 和
和![]() 可证得
可证得![]() ,根据同底的三角形面积比等于相似比即可求解
,根据同底的三角形面积比等于相似比即可求解![]() 关于
关于![]() 的函数关系;
的函数关系;
②由已知证得![]() ,得到
,得到 ,过O作OH⊥AD于H,由勾股定理得关于a的方程,解之得到AD,即可求得
,过O作OH⊥AD于H,由勾股定理得关于a的方程,解之得到AD,即可求得![]() .
.
(1)当a=1时,CG=1,BC=3,GC=2,
![]() 矩形
矩形![]() 中,
中,![]() ,
,
![]() ,AD=BC=3,
,AD=BC=3,
又![]() ,
,
![]() ,
,
![]() ,
,
∴CF=AD=3,
![]() ,
,
∵![]() ,
,![]()
∴![]() ,
,
![]() ,
,
∵ΔAOG底边OG上的高与ΔAGD底边GD的高相等,
![]()
(2)![]()
![]() 分两种情形讨论
分两种情形讨论
情形①:如图1,![]() ,
,
∵![]()
∴![]() ,又AB=8,
,又AB=8,
![]() ,
,![]()
易证![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
易证![]() ,
,![]()
∴![]()
![]()
![]()
![]()

情形②:如图2,![]() ,
,
∵∠AGB+∠BAG=90,∠AGB+∠DGC=90,
∴∠BAG=∠DGC,
![]()
![]()
![]()
![]()

(3)①∵![]() ,
,
∴![]() ,
,
又![]()
∴AE=EF,
![]()
![]()
又![]()
![]() ,
,
②![]() ,
,![]()
![]()
 ,即
,即![]() ,
,
过O作OH⊥AD于H,则有
![]() ,
,

![]() ,
,
∴AD=BC=12,
![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目