题目内容
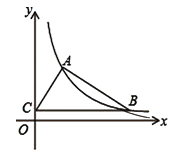
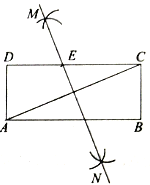
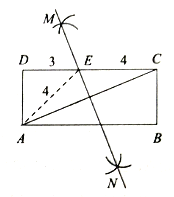
【题目】如图，在矩形
中，小聪同学利用直尺和圆规完成了如下操作：
①分别以点
和
为圆心，以大于
的长为半径作弧，两弧相交于点
和
；
②作直线
，交
于点
.
请你观察图形解答下列问题：
（1）与
的位置关系：
直线是线段的____________线；
（2）若
，
，求矩形的对角线的长.
【答案】（1）垂直平分线；（2）
【解析】
（1）利用基本作图可判断直线MN垂直平分AC；
（2）如图，连接
，则
，在
中由勾股定理求出AD2=7，在
中由勾股定理可得结论.
（1）垂直平分线
设AC与MN交于点F．连接AM、CM、AN、CN，如图，
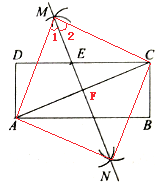
∵在△AMN和△CMN中，
，
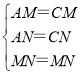∴△AMN≌△CMN（SSS）．
∴∠1=∠2．
∵AM=CM，
∴△ACM是等腰三角形．
∴MF⊥AC，AF=CF．
即MN⊥AC，MN平分AC．
（2）解：如图，连接，
则
∴在中，
∴在中，
，
，
，
.
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
