题目内容
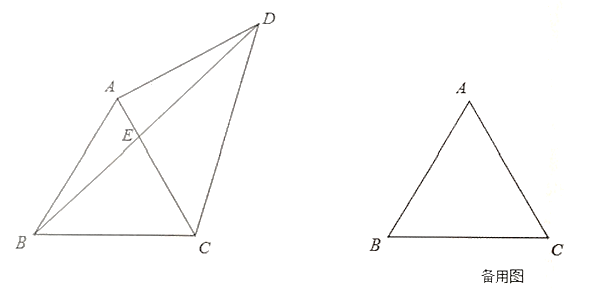
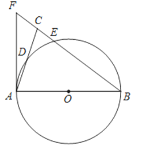
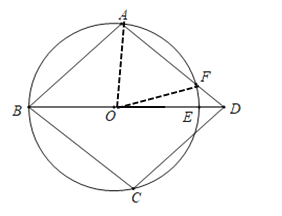
【题目】如图,在⊙O上依次有A、B、C三点,BO的延长线交⊙O于E,![]() ,过点C作CD∥AB交BE的延长线于D,连AD交⊙O于点F.
,过点C作CD∥AB交BE的延长线于D,连AD交⊙O于点F.
(1)求证:四边形ABCD是菱形;
(2)连接OA、OF.
①当∠ABC= °时,点F为![]() 的中点;
的中点;
②若∠AOF=3∠FOE且AF=3,则⊙O的半径是 .
【答案】(1)证明见解析;(2)①72;②3.
【解析】
(1)先根据圆的性质得:∠CBD=∠ABD,由平行线的性质得:∠ABD=∠CDB,根据直径和等式的性质得![]() ,则AB=BC,即可得出结论;
,则AB=BC,即可得出结论;
(2)①由题意得出∠AOF=∠EOF=m,证出∠ABE=∠ADE=m,则∠OAF=∠OFA=∠EOF+∠ADE=2m,由三角形内角和定理得出方程,解方程即可;
②先设∠FOE=x,则∠AOF=3x,根据∠ABC+∠BAD=180°,列方程求出x的值,证△AOF是等边三角形,得出OF=AF=3即可.
(1)证明:∵![]() ,
,
∴∠CBD=∠ABD,
∵CD∥AB,
∴∠ABD=∠CDB,
∴∠CBD=∠CDB,
∴CB=CD,
∵BE是⊙O的直径,
∴![]() ,
,
∴AB=BC=CD,
∵CD∥AB,
∴四边形ABCD是菱形;
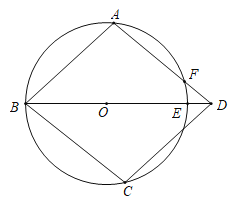
(2)解:如图所示:
①F为![]() 的中点,则∠AOF=∠EOF,
的中点,则∠AOF=∠EOF,
设∠AOF=∠EOF=m,
∵四边形ABCD是菱形,
∴AB=AD,∠ABE=∠ADE,
∵∠AOD=2∠ABE,
∴∠ABE=∠ADE=m,
∴∠OAF=∠OFA=∠EOF+∠ADE=2m,
∵∠AOF+∠OAF+∠OFA=180°,
∴2m+2m+m=180°,
∴m=36°,
∴∠ABE=72°,
即∠ABC=72°时,点F为![]() 的中点,
的中点,
故答案为:72;
②∵∠AOF=3∠FOE,
设∠FOE=x,则∠AOF=3x,
∠AOD=∠FOE+∠AOF=4x,
∵OA=OF,
∴∠OAF=∠OFA=![]() (180°﹣3x),
(180°﹣3x),
∵OA=OB,
∴∠OAB=∠OBA=2x,
∴∠ABC=4x,
∵BC∥AD,
∴∠ABC+∠BAD=180°,
∴4x+2x+![]() (180°﹣3x)=180°,
(180°﹣3x)=180°,
解得:x=20°,
∴∠AOF=3x=60°,
∵OA=OF,
∴△AOF是等边三角形,
∴OF=AF=3,
即⊙O的半径是3;
故答案为:3.
【点晴】
本题考查平行四边形和菱形的判定和性质,等边三角形的判定和性质,圆周角定理等知识,解题的关键是学会设未知数,列方程求角的度数,证明三角形是等边三角形是解题的突破点,是属于中考常考题型.