题目内容
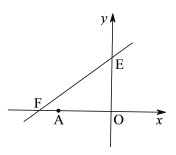
【题目】如图,直线![]() 与x轴、y轴分别相交于点F,E,点A的坐标为(-6,0),P(x,y)是直线
与x轴、y轴分别相交于点F,E,点A的坐标为(-6,0),P(x,y)是直线![]() 上的一个动点.
上的一个动点.
(1)试写出点P在运动过程中,△OAP的面积S与x的函数关系式;
(2)当点P运动到什么位置,△OAP的面积为![]() ,求出此时点P的坐标.
,求出此时点P的坐标.
【答案】(1)S=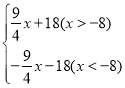 ;(2)P(-2,
;(2)P(-2,![]() )或(-14,
)或(-14,![]() )
)
【解析】
(1)设点P(x,y),将△OAP的面积表示出来,并分点P在第一、二象限和点P在第三象限两种情况进行讨论即可;
(2)分别把S=![]() 代入(1)中两种情况下的函数关系式,求出点P的横坐标,再分别代入
代入(1)中两种情况下的函数关系式,求出点P的横坐标,再分别代入![]() 中可求出点P纵坐标.
中可求出点P纵坐标.
解:(1)∵P(x,y),
∴P到x轴的距离为![]() ,
,
∵点A的坐标为(-6,0),
∴OA=6
∴S△OAP=![]() OA
OA![]()
令![]() =0,
=0,
解得x=-8,
∴F(-8,0),
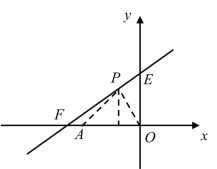
①当点P在第一、二象限时,S=![]() ×6y,
×6y,![]() ,
,
∴S=![]() x+18(x>-8),
x+18(x>-8),
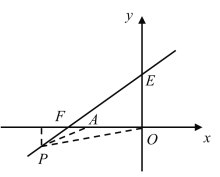
②当点P在第三象限时,S=![]() ×6(-y)
×6(-y)
∴S=-![]() x-18(x<-8),
x-18(x<-8),
∴点P在运动过程中,△OAP的面积S与x的函数关系式为:S=![]() x+18(x>-8)或S=-
x+18(x>-8)或S=-![]() x-18(x<-8),
x-18(x<-8),
或写成S=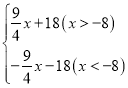 ;
;
(2)当S=![]() x+18(x>-8),△OAP的面积为
x+18(x>-8),△OAP的面积为![]() ,
,
∴![]() x+18=
x+18=![]() ,解得x=-2,代入
,解得x=-2,代入![]() ,得y=
,得y=![]() ,
,
∴P(-2,![]() )
)
当S=-![]() x-18(x<-8),△OAP的面积为
x-18(x<-8),△OAP的面积为![]() ,
,
∴-![]() x-18=
x-18=![]() ,解得x=-14,代入
,解得x=-14,代入![]() ,得y=
,得y=![]() ,
,
∴P(-14,![]() )
)
综上所述,点P的坐标为P(-2,![]() )或(-14,
)或(-14,![]() ).
).

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目