题目内容
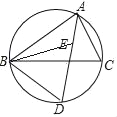
【题目】已知:⊙O为△ABC的外接圆,AB=AC,E是AB的中点,连OE,OE=![]() ,BC=8,则⊙O的半径为( )
,BC=8,则⊙O的半径为( )
A. 3 B. ![]() C.
C. ![]() D. 5
D. 5
【答案】C
【解析】
分析: 如图,作辅助线;首先求出;根据勾股定理求出DE的长度;运用射影定理即可求出AD的长度,即可解决问题.
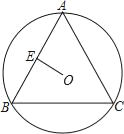
详解:如图,作直径AD,连接BD;
∵AB=AC, ∴![]() ,
,
∴AD⊥BC,BE=CE=4;
∵OE⊥AB,
∴AE=BE,而OA=OB,
∴OE为△ABD的中位线,
∴BD=2OE=5;
由勾股定理得:![]() ,
,
∴DE=3;
∵AD为⊙O的直径,
∴∠ABD=90°,由射影定理得:![]() ,而BD=5,DE=3,
,而BD=5,DE=3,
∴AD=![]() , ⊙O半径=
, ⊙O半径=![]() .故选C.
.故选C.
点睛: 本题主要考查了垂径定理、勾股定理及其应用问题;解题的关键是作辅助线,灵活运用勾股定理等几何知识点来分析、判断、推理或解答.

练习册系列答案
相关题目