题目内容
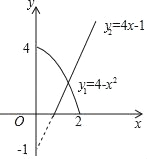
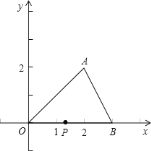
【题目】如图,已知![]() ,
,![]() .动点
.动点![]() 在线段
在线段![]() 上移动,过点
上移动,过点![]() 作直线
作直线![]() 与
与![]() 轴垂直.
轴垂直.
![]() 设
设![]() 中位于直线
中位于直线![]() 左侧部分的面积为
左侧部分的面积为![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 试问是否存在点
试问是否存在点![]() ,使直线
,使直线![]() 平分
平分![]() 的面积?若有,求出点
的面积?若有,求出点![]() 的坐标;若无,请说明理由.
的坐标;若无,请说明理由.
【答案】(1)S=-m2+6m-6;(2)存在这样的![]() 点,使
点,使![]() 平分
平分![]() 的面积,点
的面积,点![]() 的坐标为
的坐标为![]() .
.
【解析】
(1)直线l在A点左面时面积为S部分是一三角形,直线l在A点右面时面积为S部分是大三角形△OAB减去右面小三角形的面积值;(2)可以先假设存在这样的一个点,然后再验证假设是否正确,根据计算解得答案.
(1)当0≤m≤2时,
S=![]() m2;
m2;
当2<m≤3时,
S=![]() ×3×2-
×3×2-![]() (3-m)(-2m+6)=-m2+6m-6.
(3-m)(-2m+6)=-m2+6m-6.
(2)假设有这样的P点,使直线l平分△OAB的面积,
很显然0<m<2,
由于△OAB的面积等于3,
故当l平分△OAB面积时:S=![]() .
.
∴![]() m2=
m2=![]() .
.
解得m=![]() .
.
故存在这样的P点,使l平分△OAB的面积.
且点P的坐标为(![]() ,0).
,0).
∴在这样的P点,使l平分△OAB的面积,点P的坐标为(![]() ,0).
,0).

练习册系列答案
相关题目
【题目】某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:
类型 价格 | 进价(元/盏) | 售价(元/盏) |
A型 | 25 | 45 |
B型 | 40 | 70 |
(1)若商场进货款为3100元,则这两种台灯各购进多少盏?
(2)若商场在3200元的限额内购进这两种台灯,且A型台灯的进货数量不超过B型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?