题目内容
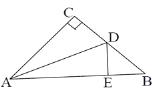
【题目】如图,在△ABC中,∠C=90°,AC=BC,D为BC上一点,且DE⊥AB于E,若DE=CD,AB=8cm,则△DEB的周长为( )
A.4cmB.8cmC.10cmD.14cm
【答案】B
【解析】
因为DE和CD相等,DE⊥AB,∠C=90°,所以AD平分CAB,可证得△ACD≌△AED,得到AC=AE,再根据△BDE为等腰直角三角形得出DE=BE,从而可得△DEB的周长.
解:∵∠C=90°,DE⊥AB,DE=CD,
∴∠C=∠AED=90°,∠CAD=∠EAD,
在Rt△ACD和Rt△AED中,
![]() ,
,
∴△ACD≌△AED(HL),
∴AC=AE,
又∵∠AED=90°,∠B=45°,
可得△EDB为等腰直角三角形,DE=EB=CD,
∴△DEB的周长=DE+ BE +DB
=CD+DB+ BE
=CB+ BE
=AC+BE
=AE+BE
=AB
=8,
故选:B.

练习册系列答案
相关题目
【题目】某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:
类型 价格 | 进价(元/盏) | 售价(元/盏) |
A型 | 25 | 45 |
B型 | 40 | 70 |
(1)若商场进货款为3100元,则这两种台灯各购进多少盏?
(2)若商场在3200元的限额内购进这两种台灯,且A型台灯的进货数量不超过B型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?