题目内容
【题目】由点P(14,1),A(a,0),B(0,a)确定的△PAB的面积为18.
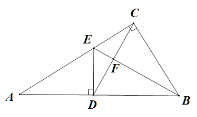
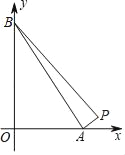
(1)如图,若0<a<14,求a的值.
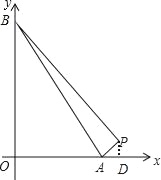
(2)如果a>14,请画图并求a的值.
【答案】(1)a1=3,a2=12;(2)a=![]() .
.
【解析】
(1)当0<a<14时,作PD⊥x轴于点D,由P(14,1),A(a,0),B(0,a)就可以表示出△ABP的面积,建立关于a的方程求出其解即可;
(2)当a>14时,作PD⊥x轴于点D,由P(14,1),A(a,0),B(0,a)就可以表示出△ABP的面积,建立关于a的方程求出其解即可.
(1)当0<a<14时,
如图,作PD⊥x轴于点D,
∵P(14,1),A(a,0),B(0,a),
∴PD=1,OD=14,OA=a,OB=a,
∴S△PAB=S梯形OBPD﹣S△OAB﹣S△ADP=![]() ×14(a+1)﹣
×14(a+1)﹣![]() a2﹣
a2﹣![]() ×1×(14﹣a)=18,
×1×(14﹣a)=18,
解得:a1=3,a2=12;
(2)当a>14时,如图,
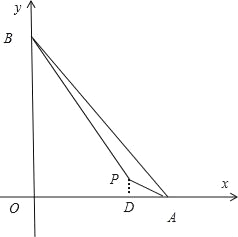
作PD⊥x轴于点D,
∵P(14,1),A(a,0),B(0,a),
∴PD=1,OD=14,OA=a,OB=a,
∴S△PAB=S△OAB﹣S梯形OBPD﹣S△ADP=![]() a2﹣
a2﹣![]() ×14(a+1)﹣
×14(a+1)﹣![]() ×1×(a﹣14)=18,
×1×(a﹣14)=18,
解得:a1=![]() ,a2=
,a2=![]() (不合题意,舍去);
(不合题意,舍去);
∴a=![]() .
.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目