题目内容
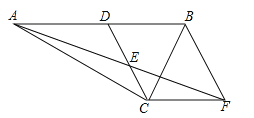
【题目】如图,在Rt△ABC中,∠ACB=![]() ,D是AB边上的一点,过D作DE⊥AB交AC于点E,BC=BD,连结CD交BE于点F.
,D是AB边上的一点,过D作DE⊥AB交AC于点E,BC=BD,连结CD交BE于点F.
(1)求证:CE=DE;
(2)若点D为AB的中点,求∠AED的度数.
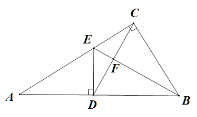
【答案】(1)证明见解析;(2)60°;
【解析】
(1)直接证明Rt△DEB≌Rt△CEB,即可解决问题.
(2)首先证明△ADE≌△BDE,进而证明∠AED=∠DEB=∠CEB,即可解决问题.
(1)∵DE⊥AB,∠ACB=![]()
∴△BCE与△BDE都是直角三角形.
在Rt△BCE与Rt△BDE中
![]()
∴Rt△BCE≌Rt△BDE(HL)
∴CE=DE
(2)∵DE⊥AB,
∴∠ADE=∠BDE=![]()
∵点D为AB的中点,
∴AD=BD
又∵DE=DE,
∴△ADE≌△BDE,
∴∠AED=∠DEB
∵△BCE≌△BDE,
∴∠CEB=∠DEB
∴∠AED=∠DEB=∠CEB,
∵∠AED+∠DEB+∠CEB=![]() ,
,
∴∠AED=![]()

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目