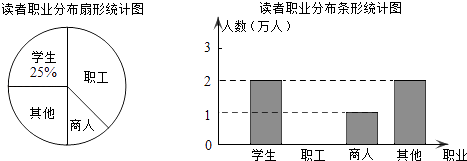
题目内容
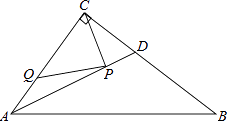
【题目】如图,在△ABC中,点P是BC上一点,PR⊥AB,PS⊥AC,垂足分别为点R、S,PR=PS,点Q是AC上一点,且AQ=PQ,
(1)求证:QP∥AR;
(2)AR、AS相等吗?说明理由.
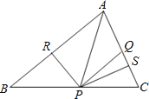
【答案】(1)证明见解析;(2)相等,理由见解析.
【解析】
(1)易证RT△APR≌RT△APS,可得∠BAP=∠1,再根据AQ=PQ,可得∠1=∠2,即可求得QP∥AR;
(2) 根据HL证明Rt△APR≌Rt△APS,即可推出AS=AR.
解:(1)如图,
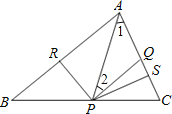
在RT△APR和RT△APS中,
![]() ,
,
∴RT△APR≌RT△APS(HL),
∴∠BAP=∠1,
∵AQ=PQ,
∴∠1=∠2,
∴∠BAP=∠2,
∴QP∥AR.
(2)AR=AS,理由如下:
∵PR⊥AB于R,PS⊥AC于S,
∴∠ARP=∠ASP=90°,
在Rt△APR和Rt△APS中,
![]() ,
,
∴Rt△APR≌Rt△APS(HL),
∴AS=AR.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某商店购进某种茶壶、茶杯共200个进行销售,其中茶杯的数量是茶壶数量的5倍还多20个.销售方式有两种:(1)单个销售;(2)成套销售.相关信息如下表:
进价(元/个) | 单个售价(元/个) | 成套售价(元/套) | |
茶壶 | 24 | a | 55 |
茶杯 | 4 | a﹣30 | |
备注:(1)一个茶壶和和四个茶杯配成一套(如图); (2)利润=(售价﹣进价)×数量 | |||
(1)该商店购进茶壶和茶杯各有多少个?
(2)已知甲顾客花180元购买的茶壶数量与乙顾客花30元购买的茶杯数量相同.
①求表中a的值.
②当该商店还剩下20个茶壶和100个茶杯时,商店将这些茶壶和茶杯中的一部分按成套销售,其余按单个销售,这120个茶壶和茶杯全部售出后所得的利润为365元.问成套销售了多少套?