题目内容
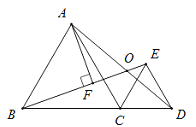
【题目】如图,△ABC与△CED均为等边三角形,且B,C,D三点共线.线段BE,AD相交于点O,AF⊥BE于点F.若OF=1,则AF的长为( )
A. 1 B. ![]() C.
C. ![]() D. 2
D. 2
【答案】C
【解析】
根据等边三角形的性质易证△BCE≌△ACD,根据全等三角形的性质可得∠CBE=∠CAD,再根据三角形外角的性质求得∠BOD=120°,即可求得∠AOF=60°,在Rt△AOF中,∠AOF=60°,OF=1,即可求得AF=![]() .
.
∵△ABC和△CDE都是等边三角形,
∴BC=AC,CE=CD,∠ACB=∠DCE=60°,
∴∠BCE=∠ACD,
在△BCE和△ACD中,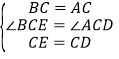 ,
,
∴△BCE≌△ACD(SAS)
∴∠CBE=∠CAD,
∵∠BOD=∠ABE+∠BAD,∠ABC=∠BAC=60°,
∴∠BOD=∠ABE+∠BAC+∠CAD=∠ABE+∠BAC+∠CBE=∠ABC+∠BAC=60°+60°=120°.
∴∠AOF=180°-∠BOD=180°-120°=60°,
在Rt△AOF中,∠AOF=60°,OF=1,
∴AF=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目