题目内容
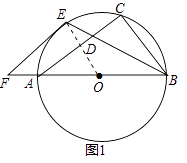
【题目】如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作⊙O切线EF交BA的延长线于F.
(1)如图1,求证:EF∥AC;
(2)如图2,OP⊥AO交BE于点P,交FE的延长线于点M.求证:△PME是等腰三角形;
(3)如图3,在(2)的条件下:CG⊥AB于H点,交⊙O于G点,交AC于Q点,如图2,若sinF= ![]() ,EQ=5,求PM的值.
,EQ=5,求PM的值.
【答案】
(1)解:证明:连接OE,
∵EF是圆的切线,
∴OE⊥FE,
∴∠F+∠FOE=90°,
∴AB为直径,
∴∠C=90°,
∴∠ABC+∠CAB=90°,
∵OE=OB,
∴∠OEB=∠OBE,
∵BE是∠B的平分线,
∴∠OBE=∠CBE,
∵∠FOE=∠OEB+∠OBE,
∴∠EOF=∠ABC,
∴∠F=∠CAB,
∴EF∥AC;
(2)解:连接OC,OE,
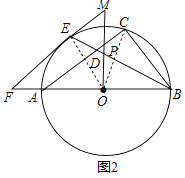
∵OP⊥AO交BE于点P,
∴∠OPB+∠OBE=90°,
∵∠OEB+∠MEB=90°,
∴∠OPB=∠MEB,
又∵∠OPB=∠EPM,
∴∠MEP=∠MPE,
∴MP=ME,
∴△PME是等腰三角形;
(3)解:连接OE,
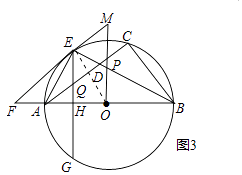
∵∠F=∠CAB,
∴sinF=sin∠CAB= ![]() ,
,
∵EG⊥AB于H点,
∴ ![]() ,
,
∴∠AEG=∠ABE,
∵∠ABE=∠EAC,
∴∠EAC=∠AEG,
∴AQ=EQ=5,
∵QH=3,AH=4,
∴EH=EQ+QH=8,
设OE=x,则OH=AO﹣AH=x﹣4,
在Rt△EHO中,x2=82+(x﹣4)2,
解得:x=10,
∴OE=10,
∵BE是∠B的平分线,
∴ ![]() ,
,
∴OE⊥AC,
∴∠CAB+∠AOD=90°,
∵∠EOM+∠AOD=90°,
∴∠EOM=∠CAB,
∴sin∠EOM= ![]() ,
,
∴tan∠EOM= ![]() =
= ![]() ,
,
∴ME= ![]() ,
,
∴PM=ME= ![]() .
.
【解析】(1)EF是圆的切线,因此;连接OE,OE⊥FE,即∠F+∠FOE=90°,AB为直径,得出∠ABC+∠CAB=90°,再证明∠OEB=∠OBE,由BE是∠B的平分线,得出∠OBE=∠CBE,再证明∠F=∠CAB,即可得出结论。
(2)连接OC,OE,由OP⊥AO得出∠OPB与∠OBE互余,∠OEB与∠MEB互余,得出∠OPB=∠MEB,再根据对顶角相等,推出MP=ME,即可得出结论。
(3)连接OE,根据已知求出sin∠CAB的值及EH的长,在Rt△EHO中,根据勾股定理建立方程,解方程求出OE的长,再证明∠EOM=∠CAB,在Rt△EPM中,求出ME的长,即可得出PM的长。
【考点精析】本题主要考查了勾股定理的概念和切线的性质定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.