题目内容
【题目】如图,A,B两个工厂位于一段直线形河的异侧,A厂距离河边AC=5km,B厂距离河边BD=1km,经测量CD=8km,现准备在河边某处(河宽不计)修一个污水处理厂E.
(1)设ED=x,请用x的代数式表示AE+BE的长;
(2)为了使两厂的排污管道最短,污水厂E的位置应怎样来确定此时需要管道多长?
(3)通过以上的解答,充分展开联想,运用数形结合思想,请你猜想![]() 的最小值为多少?
的最小值为多少?

【答案】(1)AE+BE=![]() ;(2)此时最少需要管道10km;(3)最小值为13.
;(2)此时最少需要管道10km;(3)最小值为13.
【解析】
(1)由ED=x,AC⊥CD、BD⊥CD,根据勾股定理可用x表示出AE+BE的长;(2)根据两点之间线段最短可知连接AB与CD的交点就是污水处理厂E的位置.过点B作BF⊥AC于F,构造出直角三角形,利用勾股定理求出AB的长即可;(3)根据AE+BE=![]() +
+![]() =AB=10;即可猜想所求代数式的值.
=AB=10;即可猜想所求代数式的值.
(1)在Rt△ACE和Rt△BDE中,根据勾股定理可得AE=![]() ,BE=
,BE=![]() ,
,
∴AE+BE=![]() +
+![]() ;
;
(2)根据两点之间线段最短可知连接AB与CD的交点就是污水处理厂E的位置.
过点B作BF⊥AC于F,则有BF=CD=8,BD=CF=1.
∴AF=AC+CF=6.
在Rt△ABF中,BA=![]() =
=![]() =10,
=10,
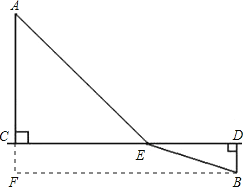
∴此时最少需要管道10km.
(3)根据以上推理,设ED=x.AC=3,DB=2,CD=12.
∴当A、E、B共线时求出AB的值即为原式最小值.
当A、E、B共线时![]() +
+![]() =
=![]() =13,即其最小值为13.
=13,即其最小值为13.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目