题目内容
【题目】四边形ABCD的对角线交于点E,且AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
(1)利用图1,求证:四边形ABCD是菱形.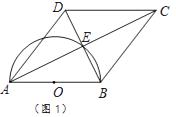
(2)如图2,若CD的延长线与半圆相切于点F,且直径AB=8.
①△ABD的面积为 .
② ![]() 的长 .
的长 . 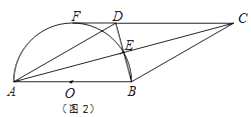
【答案】
(1)解:∵AE=EC,BE=ED,
∴四边形ABCD是平行四边形.
∵AB为直径,且过点E,
∴∠AEB=90°,即AC⊥BD.
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
(2)16,![]() π
π
【解析】(2)①连结OF.
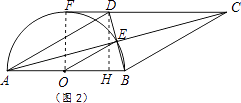
∵CD的延长线与半圆相切于点F,
∴OF⊥CF.
∵FC∥AB,
∴OF即为△ABD中AB边上的高.
∴S△ABD= ![]() AB×OF=
AB×OF= ![]() ×8×4=16,
×8×4=16,
∵点O是AB中点,点E是BD的中点,
∴S△OBE= ![]() S△ABD=4.②过点D作DH⊥AB于点H.
S△ABD=4.②过点D作DH⊥AB于点H.
∵AB∥CD,OF⊥CF,
∴FO⊥AB,
∴∠F=∠FOB=∠DHO=90°.
∴四边形OHDF为矩形,即DH=OF=4.
∵在Rt△DAH中,sin∠DAB= ![]() =
= ![]() ,
,
∴∠DAH=30°.
∵点O,E分别为AB,BD中点,
∴OE∥AD,
∴∠EOB=∠DAH=30°,
∴ ![]() 的长度=
的长度= ![]() =
= ![]() π.
π.
所以答案是:16, ![]() π.
π.
【考点精析】通过灵活运用圆周角定理和切线的性质定理,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】核桃和枣是我省著名的农特产,它们营养丰富,有益人体健康,深受老百姓喜爱。某超市从农贸批发市场批发核桃和枣进行零售,批发价和零售价格如下表所示:
名称 | 核桃 | 枣 |
批发价(元/ | 12 | 9 |
零售价(元/ | 18 | 12 |
请解答下列问题.
(1)第一天,该超市从批发市场批发核桃和枣共350![]() ,用去了3600元钱,求当天核桃和枣各批发多少kg?
,用去了3600元钱,求当天核桃和枣各批发多少kg?
(2)第二天,该超市用3600元钱仍然批发核桃和枣(批发价和零售价不变),要想将第二天批发的核桃和枣全部售完后,所获利润不低于40%,则该超市第二天至少批发核桃多少kg?