题目内容
【题目】阅读下面材料:
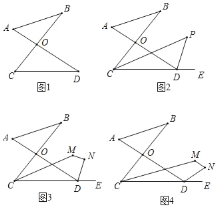
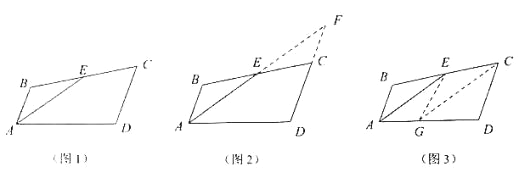
小明遇到这样一个问题:如图 1,在四边形 ABCD 中,E 是 BC 的中点,AE 是∠BAD 的平分线,AB∥DC,求证:AD=AB+DC. 小明发现以下两种方法:
方法 1:如图 2,延长 AE、DC 交于点 F;
方法 2:如图 3,在 AD 上取一点 G 使 AG=AB,连接 EG、CG.
(1)根据阅读材料,任选一种方法,证明:AD=AB+DC; 用学过的知识或参考小明的方法,解决下面的问题:
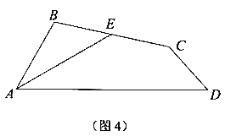
(2)如图 4,在四边形 ABCD 中,AE 是∠BAD 的平分线,E 是 BC 的中点,∠BAD=60°,∠ABC=180°-![]() ∠BCD,求证:CD=CE.
∠BCD,求证:CD=CE.
【答案】(1)见解析;(2)见解析.
【解析】
(1)方法1:如图2,延长AE、DC交于点F,证明△ABE≌△FCE(ASA)即可解决问题
方法2:如图3,在AD上取一点G使AG=AB,连接EG、CG.想办法证明DC=DG即可解决问题;
(2)如图4中,作CM∥AB交AE的延长线于M,CM交AD于N,连接EN.只要证明△CNE≌△CND(ASA)即可解决问题;
(1)方法1:如图2,延长AE、DC交于点F;
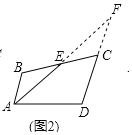
∵AB∥DF,
∴∠B=∠ECF,
∵BE=EC,∠BEA=∠CEF,
∴△ABE≌△FCE(ASA),
∴AB=CF,
∵EA平分∠BAD,
∴∠BAE=∠DAF=∠F,
∴AD=DF,
∴AD=CD+AB.
方法2:如图3,在AD上取一点G使AG=AB,连接EG、CG.
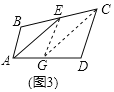
∵AB=AG,∠BAE=∠GAE,AE=AE,
∴△BAE≌△GAE(SAS),
∴BE=EG=EC,∠AEB=∠AEG,
∴∠EGC=∠ECG,
∵∠BEG=∠EGC+∠ECG,
∴∠BEA=∠ECG,
∴AE∥CG,
∴∠EAG=∠CGD,
∵AB∥CD,AE∥CG,
∴∠BAE=∠DCG,
∴∠DCG=∠DGC,
∴CD=DG,
∴AD=AB+CD.
(2)证明:如图4中,作CM∥AB交AE的延长线于M,CM交AD于N,连接EN.
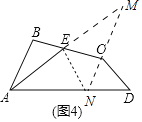
由(1)可知:AN=NM,AE=EM,
∴EN平分∠ANM,
∵∠BAD=60°,MN∥AB,
∴∠MND=∠BAD=60°,
∴∠ENM=∠ENA=60°,
∴∠CND=∠CNE,
∵∠B+∠ECN=180°,∠ABC=180°-![]() ∠BCD,
∠BCD,
∴∠NCE=∠NCD,∵CN=CN,
∴△CNE≌△CND(ASA),
∴CE=CD.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案