题目内容
【题目】每年11月的最后一个星期四是感恩节,小龙调查了初三年级部分同学在感恩节当天将以何种方式表达感谢帮助过自己的人.他将调查结果分为如下四类:A类﹣﹣当面致谢;B类﹣﹣打电话;C类﹣﹣发短信息或微信;D类﹣﹣写书信.他将调查结果绘制成如图不完整的扇形统计图和条形统计图:
请你根据图中提供的信息完成下列各题: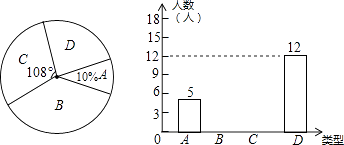
(1)补全条形统计图;
(2)在A类的同学中,有3人来自同一班级,其中有1人学过主持.现准备从他们3人中随机抽出两位同学主持感恩节主题班会课,请你用树状图或表格求出抽出的两人都没有学过主持的概率.
【答案】
(1)解:由题意可知总人数=5÷10%=50(人),所以D类所占的百分比为12÷50×100%=24%,C所占的百分比= ![]() =30%,所以C所占的人数=50×30%=15(人);
=30%,所以C所占的人数=50×30%=15(人);
B所占的百分比=1﹣10%﹣24%﹣30%=36%,B所占的人数=50×36%=18(人),由此补全统计图可得:
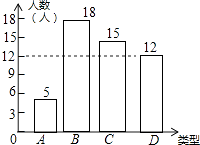
(2)解:设两个没学过主持的学生别标记为A1,A2,学过主持的学生标记为B1,列表如下:
A1 | A2 | B1 | |
A1 | (A1,A2) | (A1,B1) | |
A2 | (A2,A1) | (A2,B1) | |
B1 | (B1,A1) | (B1,A2) |
P(两人都没有学过主持)= ![]() =
= ![]()
【解析】(1)由A类的人数和百分比求出总人数,即可求出D类所占的百分比、C所占的百分比、C所占的人数、B所占的百分比、B所占的人数。就可补全统计图。
(2)先设两个没学过主持的学生别标记为A1,A2,学过主持的学生标记为B1再画出树状图或列表,根据概率公式即可求解。
【考点精析】利用扇形统计图和条形统计图对题目进行判断即可得到答案,需要熟知能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.

【题目】如图是连续十周测试甲、乙两名运动员体能情况的折线统计图,教练组规定:体能测试成绩70分以上(包括70分)为合适.
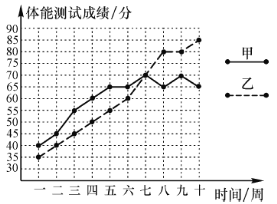
(1)请根据图中所提供的信息填写下表:
平均数 | 中位数 | 体能测试成绩合格次数(次) | |
甲 | 65 | ||
乙 | 60 |
(2)请从下面两个不同的角度对运动员体能测试结果进行判断:①依据平均数与成绩合格的次数比较甲和乙,哪个的体能测试成绩较好;②依据平均数与中位数比较甲和乙,哪个的体能测试成绩较好;
(3)依据折线统计图和成绩合格的次数,分析哪位运动员体能训练的效果较好.