��Ŀ����
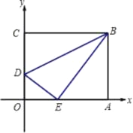
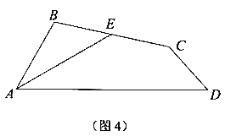
����Ŀ����1����ͼ1��ͼ�����ǰ�����Ϊ��8���Ρ������A����B����C����D�ĸ��ǵ�������ϵ���� ����
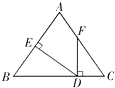
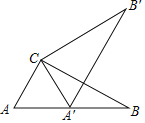
��2����ͼ2������BCD����ADE�Ľ�ƽ����CP��DP���ڵ�P�����P���A����B��������ϵΪ��P���� ����
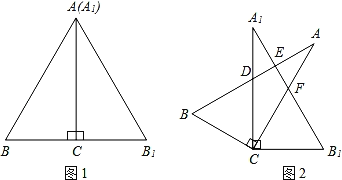
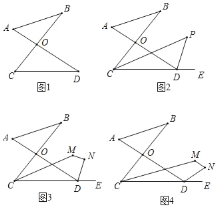
��3����ͼ3��CM��DN�ֱ�ƽ�֡�BCD����ADE������A+��B��80��ʱ�������M+��N�Ķ��������ѣ�������������ֱ�������������ۣ���
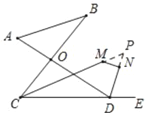
��4����ͼ4�������MCD��![]() ��BCD����NDE��
��BCD����NDE��![]() ��ADE������A+��B��n��ʱ�������M+��N�Ķ�����
��ADE������A+��B��n��ʱ�������M+��N�Ķ�����
���𰸡���1����A+��B����C+��D����2��90�㩁![]() ����A+��B������3����CMN+��DNM��230�㣻��4����CMN+��DNM��240�㩁
����A+��B������3����CMN+��DNM��230�㣻��4����CMN+��DNM��240�㩁![]() n�㣮
n�㣮
��������
��1���������ε��ڽǺ;�Ϊ180�㼰ͼ����AOB����CODΪ�Զ��ǿ�֪��A+��B����C+��D��
��2������PCD��x����ADP��y����CP��DP��Ϊ��ƽ���߿ɵ���BCD��2x����ADE��2y��������������ǺͶ����ɵ���P����PDE����PCD��y��x����COD����ODE����BCD��2y��2x����������COD��2��P�����������ڽǺͶ����Լ���COD����AOB�ǶԶ��ǿɵã���COD+��A+��B��180����������COD��2��P�����滻�ɵ���P��90����![]() ����A+��B����
����A+��B����
��3���ӳ�CM��DN���ڵ�P������һ�ʽ��ۿ�֪��P��90����![]() ����A+��B�������������������������P��50�������������ڽǺͶ����ɵ���PMN+��PNM��130��������M+��N��360��-(��PMN+��PNM)=360����130����230����
����A+��B�������������������������P��50�������������ڽǺͶ����ɵ���PMN+��PNM��130��������M+��N��360��-(��PMN+��PNM)=360����130����230����
��4���ӳ�CM��DN���ڵ�P������PCD��x����ADP��2y������MCD��![]() ��BCD����NDE��
��BCD����NDE��![]() ��ADE����NDE��y����BCD=3x��������������ǺͶ����Լ��ڽǺͶ�������P��y��x����COD��3y��3x������COD��3��P�����������ڽǺͶ����ɵ�3��P+��A+��B��180���������֪��A+��B��n�������֪��P��
��ADE����NDE��y����BCD=3x��������������ǺͶ����Լ��ڽǺͶ�������P��y��x����COD��3y��3x������COD��3��P�����������ڽǺͶ����ɵ�3��P+��A+��B��180���������֪��A+��B��n�������֪��P��![]() ��ͬ������CMN+��DNM��360����(��PMN+��PNM)=360��-��120��+
��ͬ������CMN+��DNM��360����(��PMN+��PNM)=360��-��120��+![]() ����240����
����240����![]() ��
��
�⣺��1����ͼ1������AOB�У���A+��B+��AOB��180����
����COD����C+��D+��COD��180����
�ߡ�AOB����COD��
���A+��B����C+��D��
�ʴ�Ϊ����A+��B����C+��D��
��2������PCD��x����ADP��y��
��CP��DP�ֱ�ƽ����BCD����ADE��
���BCD��2x����ADE��2y��
�ߡ�P����PDE����PCD��y��x��
��COD����ODE����BCD��2y��2x��
���COD��2��P��
�ߡ�COD+��A+��B��180����
��2��P+��A+��B��180����
���P��90����![]() ����A+��B����
����A+��B����
�ʴ�Ϊ��90����![]() ����A+��B����
����A+��B����
��3���ӳ�CM��DN���ڵ�P��
�ɣ�2��֪����P��90����![]() ����A+��B����
����A+��B����
�ߡ�A+��B��80����
���P��50����
���PMN+��PNM��130����
���CMN+��DNM��360����130����230����
��4���ӳ�CM��DN���ڵ�P��

����PCD��x����ADP��2y��
�ߡ�MCD��![]() ��BCD����NDE��
��BCD����NDE��![]() ��ADE��
��ADE��
����NDE��y����BCD=3x��
����P��y��x����COD��3y��3x��
���COD��3��P��
��3��P+��A+��B��180����
�ߡ�A+��B��n����
���P��![]() ��
��
���PMN+��PNM��180����![]() ��120��+
��120��+![]() ��
��
���CMN+��DNM��360������120��+![]() ����240����
����240����![]() ��
��

����Ŀ������ij��ѧ�������й���У�����������ִ������ߡ����в����ݳ����ɼ�����ѡ��5��ѡ����ɳ��д����Ӻ��д����Ӳμ�ѧУ�����������Ӹ�ѡ����5��ѡ�ֵľ����ɼ���ͼ��ʾ��

��1������ͼʾ��д�±���
ƽ�������֣� | ��λ�����֣� | �������֣� | |
���в� | 85 | ||
���в� | 85 | 100 |
��2��������ӳɼ���ƽ��������λ���������ĸ��ӵľ����ɼ��Ϻã�
��3���������Ӿ����ɼ��ķ���ж���һ��������ѡ�ֳɼ���Ϊ�ȶ���
����Ŀ����ɽ��������A��B�����й�·����·��������ҹ�����A�ع���һ��ÿ��1000Ԫ��ԭ�Ͼ���·120km��·10km�˻ع������Ƴ�ÿ��8000Ԫ�IJ�Ʒ����·110km��·20km���۵�B�أ���֪��·���˼�Ϊ1.2Ԫ/���֡�ǧ��)����·���˼�Ϊ1.5Ԫ/(�֡�ǧ��)�������������乲֧����·�˷�124800Ԫ����·�˷�19500Ԫ��
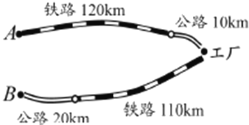
��1����ԭ����x�֣���Ʒ��y�֣���������������ϵ��д�±�
ԭ��x�� | ��Ʒy�� | �ϼƣ�Ԫ�� | |
��·�˷� | 124800 | ||
��·�˷� | 19500 |
�����ϱ��з�������ԭ�ϺͲ�Ʒ��������
��2��������Ʒ�����ۿ��ԭ�Ϸ�������ѵĺͶ����Ԫ?