题目内容
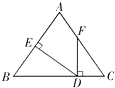
【题目】如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．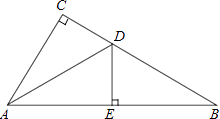
（1）求证：△ACD≌△AED；
（2）若∠B=30°，CD=1，求BD的长．
【答案】
（1）证明：∵AD平分∠CAB，DE⊥AB，∠C=90°，
∴CD=ED，∠DEA=∠C=90°，
∵在Rt△ACD和Rt△AED中
∴Rt△ACD≌Rt△AED（HL）
（2）解：∵DC=DE=1，DE⊥AB，
∴∠DEB=90°，
∵∠B=30°，
∴BD=2DE=2
【解析】（1）根据角平分线上的点到角两边的距离相等，得出CD=ED，可证Rt△ACD≌Rt△AED。
（2）根据再直角三角形中，30°角所对的直角边等于斜边的一半，即可求出DB的长。
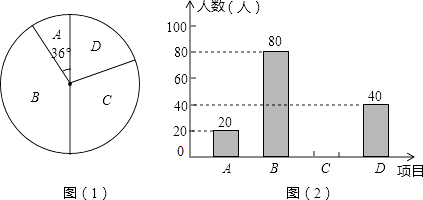
【题目】八年级一班开展了“读一本好书”的活动，班委会对学生阅读书籍的情况进行了问卷调查，问卷设置了“小说”、“戏剧”、“散文”、“其他”
四个类别，每位同学仅选一项，根据调查结果绘制了不完整的频数分布表和扇形统计图．根据图表提供的信息，回答下列问题：
类别 | 频数（人数） | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | m | 1 |
（1）计算m=；
（2）在扇形统计图中，“其他”类所占的百分比为；
（3）在调查问卷中，甲、乙、丙、丁四位同学选择了“戏剧”类，现从中任意选出2名同学参加学校的戏剧社团，请用画树状图或列表的方法，求选取的2人恰好是乙和丙的概率．
【题目】为了提高学生书写汉字的能力，增强保护汉字的意识，我市举办了首届“汉字听写大赛”，经选拔后有50名学生参加决赛，这50名学生同时听写50个汉字，若每正确听写出一个汉字得1分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
组别 | 成绩x分 | 频数（人数） |
第1组 | 25≤x＜30 | 4 |
第2组 | 30≤x＜35 | 8 |
第3组 | 35≤x＜40 | 16 |
第4组 | 40≤x＜45 | a |
第5组 | 45≤x＜50 | 10 |
请结合图表完成下列各题：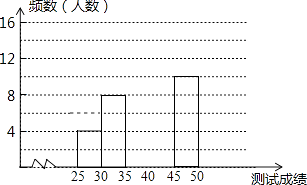
（1）求表中a的值；
（2）请把频数分布直方图补充完整；
（3）若测试成绩不低于40分为优秀，则本次测试的优秀率是多少？
（4）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小宇与小强两名男同学能分在同一组的概率．
【题目】青山化工厂与A、B两地有公路、铁路相连，这家工厂从A地购买一批每吨1000元的原料经铁路120km和公路10km运回工厂，制成每吨8000元的产品经铁路110km和公路20km销售到B地．已知铁路的运价为1.2元/（吨·千米)，公路的运价为1.5元/(吨·千米)，且这两次运输共支出铁路运费124800元，公路运费19500元．
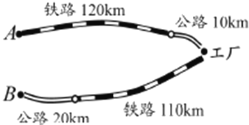
（1）设原料重x吨，产品重y吨，根据题中数量关系填写下表
原料x吨 | 产品y吨 | 合计（元） | |
铁路运费 | 124800 | ||
公路运费 | 19500 |
根据上表列方程组求原料和产品的重量．
（2）这批产品的销售款比原料费与运输费的和多多少元?
