Question

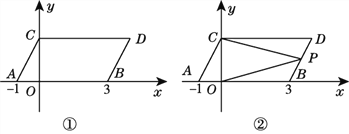
【题目】如图①，在平面直角坐标系中，点A，B的坐标分别为(－1，0)，(3，0)，现同时将点A，B分别向上平移2个单位长度，再向右平移1个单位长度，分别得到点A，B的对应点C，D，连接AC，BD，CD.

(1)求点C，D的坐标及S四边形ABDC.

(2)在y轴上是否存在一点Q，连接QA，QB，使S△QAB＝S四边形ABDC？若存在这样一点，求出点Q的坐标；若不存在，试说明理由．

(3)如图②，点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时(不与B，D重合)，给出下列结论：①的值不变，②的值不变，其中有且只有一个是正确的，请你找出这个结论并求其值．

Answer 1

【答案】（1）C(0，2)，D(4，2)，8；（2）Q点的坐标为(0，4)或(0，－4)；（3）见解析

【解析】试题分析：（1）依题意知，将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，故C、D两点点y值为2. 所以点C，D的坐标分别为C（0，2），D(4，2) ，

四边形ABDC的面积S四边形ABDC＝CO×AB=2×4=8

（2）（2）在y轴上是否存在一点P，使S△PAB=S四边形ABDC．理由如下：

设点P到AB的距离为h，

S△PAB=×AB×h=2h，

由S△PAB=S四边形ABDC，得2h=8，

解得h=4，

∴P（0，4）或（0，-4）．

（3）①是正确的结论，过点P作PQ∥CD，

因为AB∥CD，所以PQ∥AB∥CD（平行公理的推论）

∴∠DCP＝∠CPQ，∵∠BOP＝∠OPQ(两直线平行，内错角相等)，

∴∠DCP＋∠BOP＝∠CPQ +∠OPQ ＝∠CPO

所以＝=1．