题目内容
【题目】如图，在
中，
与相切于点
，直径
与交于点
，弦
与
交于点
，
，
，
，则的长为________.
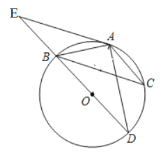
【答案】
【解析】
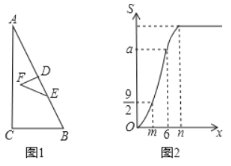
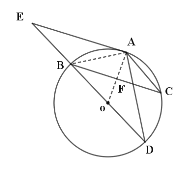
连接OA，AB，根据∠CAD和∠E的度数，以及同弧所对的圆周角相等得出∠CBD=∠E，从而得到AE∥BC，可得△OAB为等边三角形，利用垂径定理得出AB=AC，BF=CF，结合BC=2与勾股定理求出AB和BO的长， 即可得到结果.
解：连接OA，AB，F为AO和BC的交点，
∵∠CAD=∠E=30°，
∴∠CBD=∠E=30°，
∴AE∥BC，
∵AE与圆O相切，
∴AO⊥AE，
∴∠OAE=∠BFO=90°，
∴∠BOF=60°，
∴△OAB为等边三角形，
∵OA⊥BC，BC=2，
∴OA垂直平分BC，
∴BF=CF=1，设OF=x，则OB=2x，
在△BOF中，有
，
解得：x=
，
∴AB=AC=2x=，
故答案为：.
练习册系列答案
相关题目
【题目】某服装公司有
型童装80件，
型童装120件，分配给下属的“万达”和“万象城”两个专卖店销售，其中140件给万达店，60件给万象城店，且都能卖完，两商店销售这两种童装每件的利润（元）如表：
|
| |
万达店 | 100 | 80 |
万象城店 | 80 | 90 |
（1）设分配给万达店型产品
件（
），请在下表中用含的代数式填写：
|
| |
万达店 |
| ______ |
万象城店 | ______ | ______ |
若记这家服装公司卖出这200件产品的总利润为
（元），求关于的函数关系．
（2）现要求总利润不低于18140元，请说明有多少种不同分配方案，并写出各种分配方案．
