题目内容
【题目】如图,图![]() 正方形网格,每个小正方形的边长为1,请按要求画出下列图形,所画图形的各个顶点均在所给小正方形的顶点上.
正方形网格,每个小正方形的边长为1,请按要求画出下列图形,所画图形的各个顶点均在所给小正方形的顶点上.
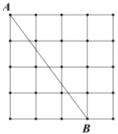
(1)在图中画出一个直角![]() ,并且其面积为5;
,并且其面积为5;
(2)在图中画出一个等腰直角![]() ;
;
(3)连接![]() ,直接写出
,直接写出![]() 的长.
的长.
【答案】(1)见详解;(2)见详解;(3)![]()
【解析】
(1)利用直角三角的定义结合勾股定理得出符合题意的答案;
(2)直接利用等腰直角三角形的定义结合勾股定理得出答案;
(3)连接BD,由勾股定理即可求出BD的长度.
解:(1)如图所示:△ABC为所求;

由勾股定理,得:![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴△ABC是直角三角形;
∴△ABC的面积为:![]() ;
;
(2)如图所示,△ACD为所求;

由(1)知,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴△ACD是等腰直角三角形;
(3)如图:

由勾股定理,得![]() .
.

练习册系列答案
相关题目
【题目】![]() 城有肥料
城有肥料![]() ,
,![]() 城有肥料
城有肥料![]() .现要把这些肥料全部运往
.现要把这些肥料全部运往![]() 、
、![]() 两乡,
两乡,![]() 乡需要肥料240t,
乡需要肥料240t,![]() 乡需要肥料
乡需要肥料![]() ,其运往
,其运往![]() 、
、![]() 两乡的运费如下表:
两乡的运费如下表:
两城/两乡 | C/(元/ | D/(元/ |
| 20 | 24 |
| 15 | 17 |
设从![]() 城运往
城运往![]() 乡的肥料为
乡的肥料为![]() ,从
,从![]() 城运往两乡的总运费为
城运往两乡的总运费为![]() 元,从
元,从![]() 城运往两乡的总运费为
城运往两乡的总运费为![]() 元
元
(1)分别写出![]() 、
、![]() 与
与![]() 之间的函数关系式(不要求写自变量的取值范围);
之间的函数关系式(不要求写自变量的取值范围);
(2)试比较![]() 、
、![]() 两城总运费的大小;
两城总运费的大小;
(3)若![]() 城的总运费不得超过4800元,怎样调运使两城总费用的和最少?并求出最小值.
城的总运费不得超过4800元,怎样调运使两城总费用的和最少?并求出最小值.